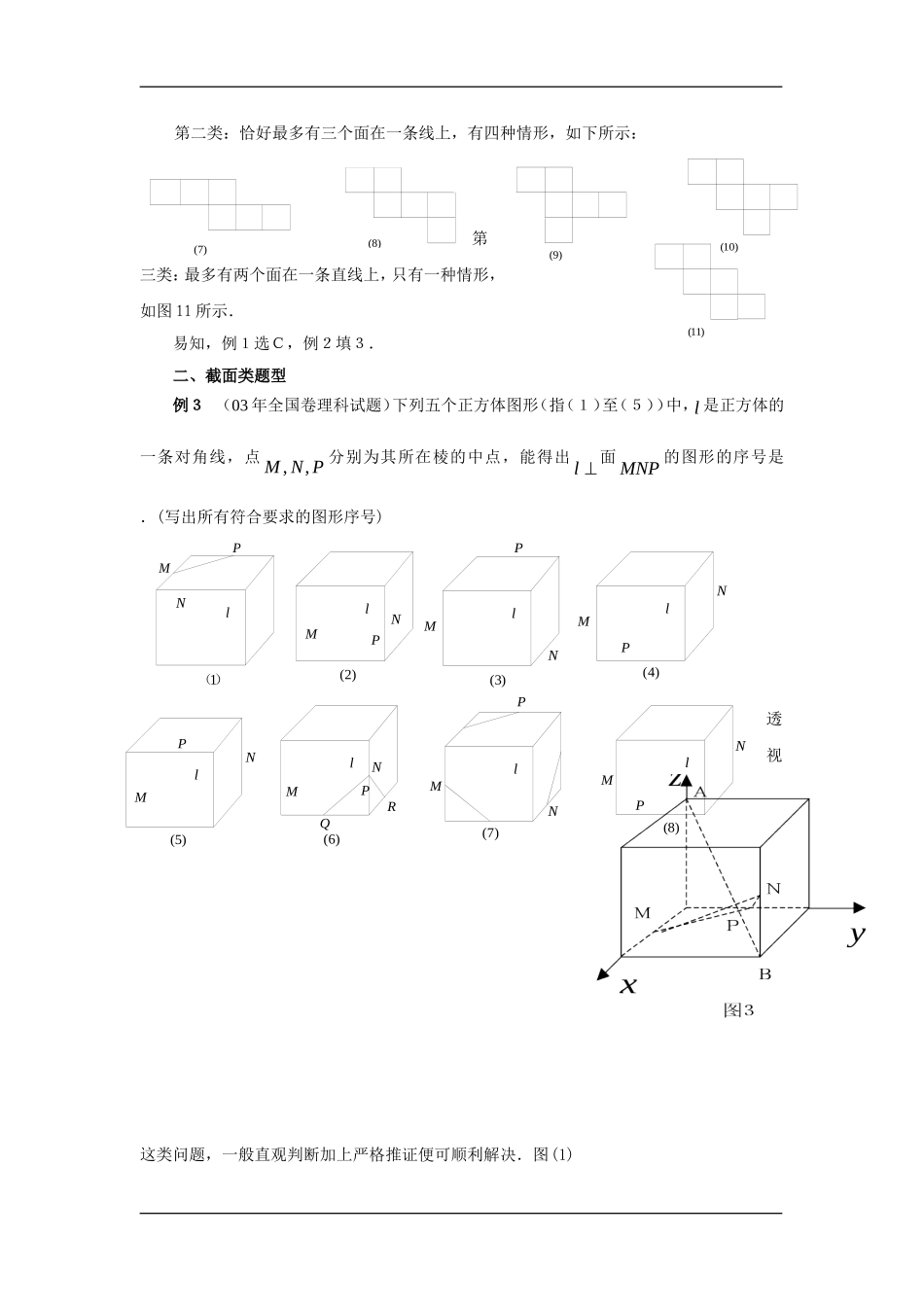
河南省滑县教师进修学校申治国的文章之《透视关于正方体的高考常见题型》正方体是常见的也是重要的几何体,依托正方体为载体,可以设计很多对考生既觉得熟悉又有点觉得陌生的高考试题,下面,对在高考中曾经出现过的相关高考题型做以整理,加以透视.一、展开图类题型这类问题渗透了平面图形与空间图形的对应性,备考前应该在课下多动手作模型,多观察,培养好自己的空间想象能力,进而达到考试时不操作也一样可以想象出来.例1(01年北京春季高考试题)图1是正方体的平面展开图,在这个正方体中,①BM与ED平行;②CN与BE是异面直线;③CN与BM成60角;④DM与BN垂直.以上四个命题中,正确命题的序号是().A.①②③B.②④C.③④D.②③④例2(02年上海春季高考试题)图2表示一个正方体表面的一种展开图,图中的四条线段AB、CD、EF和GH在原正方体中相互异面的有对.透视:上面两个高考题给出的正方体的展开图是不同的,深入思考,不难发现正方体共有三大类11种不同情形的展开图.第一类:有四个面在一条线上,有6种情形,如下所示:(1)(2)(3)(4)(5)(6)第二类:恰好最多有三个面在一条线上,有四种情形,如下所示:第三类:最多有两个面在一条直线上,只有一种情形,如图11所示.易知,例1选C,例2填3.二、截面类题型例3(03年全国卷理科试题)下列五个正方体图形(指(1)至(5))中,l是正方体的一条对角线,点,,MNP分别为其所在棱的中点,能得出l面MNP的图形的序号是.(写出所有符合要求的图形序号)透视这类问题,一般直观判断加上严格推证便可顺利解决.图(1)(7)(8)(9)(10)(11)MNPl1()MNPl(2)MNPl(3)MNPl(4)MNPl(5)QNPlRM(6)NPlM(7)NPlM(8)本身就是截面,易知符合要求;对于图(2),如图(6),可以考虑截面NQR,,QR也是棱的中点,它与直线l是垂直的,而过一点直线的垂面只有一个,截面NQR与三角形NMP不共面,故(2)不符合;图(3)可以仿图(2)进行思考,图(3)可补成截面形式,如图(7);图(4)和图(5)则可补成相同的截面,如图(8).由图可知,图(3)不符合,图(4)和图(5)符合.如果借助解决立体几何问题的“新武器”空间直角坐标系,则问题更容易得到解决.例如对图(2)的判断,构造图3,设正方体的棱长是1,则各点的坐标分别是1(0,0,1),(1,1,0),(,0,0),2ABM1(1,1,),2N1(0,,0)2P,故(1,1,1)AB�,11(,1,)22MN�,此时,由11(1,1,1)(,1,)1022ABMN�,可知,直线AB与直线MN不垂直,则直线AB一定不垂直平面MNP,否则,直线AB与直线MN应该垂直.其它可做类似的判断.三、射影类题型例4(00年全国新课程卷)如图4,E、F分别为正方体的面11AADD、面11BBCC的中心,则四边形EBFD1在该正方体的面上的射影可能是_______(要求:把可能的图的序号都填上).透视:只需首先找出四边形的顶点在各面的射影,可知②③符合要求.四、概念类题型例5(02年北京高考试题)设命题甲:“直四棱柱ABCD—A1B1C1D1中,平面ACB1与对角面BB1D1D垂直”;命题乙:“直四棱柱ABCD—A1B1C1D1是正方体”.那么,甲是乙的().A.充分必要条件B.充分非必要条件C.必要非充分条件D.既非充分又非必要条件透视:本题主要考查对正方体有关概念的掌握.如图5,先构造正方体ABCD—A1B1C1D1,可知平面ACB1与对角面BB1D1D垂直;在对角面BB1D1D中,EF分别在B1D1和BD上,且1//EFBB,直四棱柱ABCF—A1B1C1E中,平面ACB1与对角面BB1EF垂直,但直四棱柱ABCF—A1B1C1E不是正方体.故选C.这里体现了构造思想的应用.五、计数类题型例6(02年全国高考卷)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有().A.8种B.12种C.16种D.20种透视:正方体的6个面不相邻则相对,先选对面有3种方法,每种情形又可以从剩下的4个面中任选一面作为第3面,故有3×4=12种选法.例7(04年湖南高考试题)从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为().A.56B.52C.48D.40透视:由分类计数原理,以两棱为直角边的直角三角形有3×8=24个(每个顶点处有3个);以一条棱和一条面对角线为直角边的直角三角形有2×12=24个(每条棱有2个符合条件的三角形)...