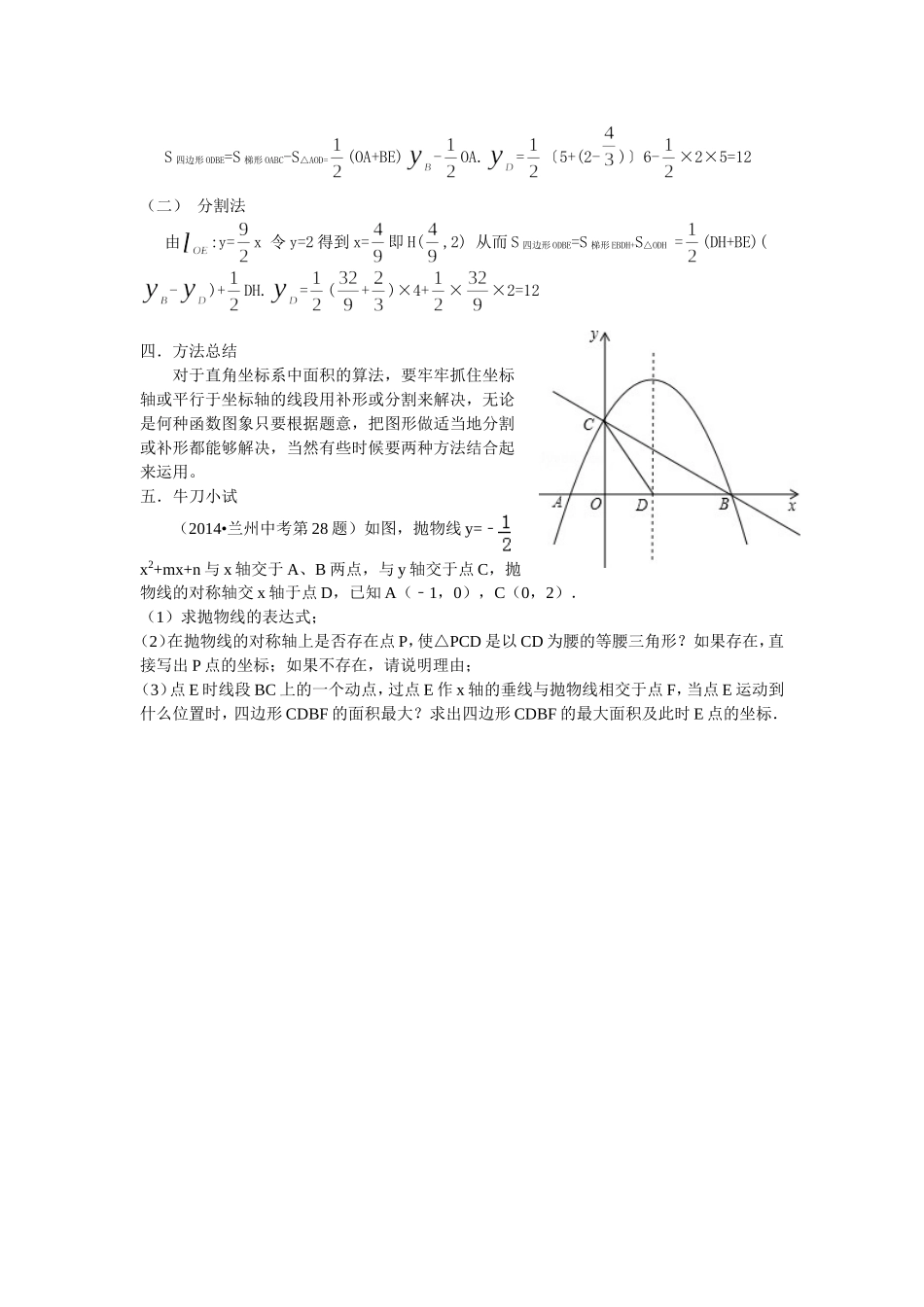
关于直角坐标系中面积计算的两种策略田英东中文摘要:为了解决学生能在直角坐标系中准确快速地计算出图形的面积,这篇文章紧紧围绕直角坐标系中点的定义和一般图形面积的计算方法,探讨出比较实用的方法,即恰当地利用坐标轴或平行于坐标轴的线段对图形做分割或补形,由点的坐标意义及所构造出的平行于坐标轴的线段来做底或高对面积进行计算,这样做的效果是学生感到化深奥为浅显的作用,解决学生在这方面的困惑。关键词:图形面积,分割,补形我们知道函数性质是中考必考的考点,而对函数图象中有关面积问题的考查成为近年来中考命题热点,其解法是根据图形的特征,有两种策略可以实施,即补形和分割。补形是把图形补为规则的图形后再减去多余的部分,分割是把图形分割为几个易于算出面积的部分,然后各个面积相加。无论补形还是分割,都要利用坐标轴或平行于坐标轴的线段做图形的底,点的横(纵)坐标的绝对值或差的绝对值做图形的高,这样可以容易计算出面积来。一.例题呈现(2014•河南中考第20题)如图,在直角梯形OABC中,BC//AO,∠AOC=900,点A、B的坐标分别为(5,0)、(2,6),点D为AB上一点,且BD=2AD.双曲线y=(x>0)经过点D,交BC于点E.(1)求双曲线的解析式;(2)求四边形ODBE的面积。二.问题分析这是一个考察反比例函数图形与性质的题目,首先由题意结合图形,利用相似,容易得到D(4,2)从而双曲线的解析式为,E(,6)。对于四边形OBDE的面积问题,这个图形为不规则的四边形,限于本题给的图形比较容易观察出来,所以在这里只是方法的讲解,不拘于原来的图形了,如果按照补形的办法可以延长BD于X轴交于点A,四边形ODBE就补为梯形OABE,然后就有S四边形ODBE=S梯形OABC-S△AOD;或者既延长BD于X轴交点A,又延长BE交Y轴于点C,过A点做平行Y轴射线与CB的延长线交于点F,这样四边形ODBE被补形为矩形OAFC,这样便有了S四边形ODBE=S矩形OAFC-S△OCE-S△AOD-;S△ABF,当然由于题目中所给点的坐标都可以算出来,所以也可延长AB,OE相交点G,补四边形ODBE为△OAG,从而就有S四边形ODBE=S△OAG-S△EBG-S△AOD。从上面的分析过程可以看出无论何种的补形都用到了坐标轴或平行于坐标轴的线段。当然如果按照分割法来做,分割的原则还是要从图形上的某个点开始做出平行于坐标轴的线段,从而将图形分为几个易于计算面积的小图形。例如本题可以过D作平行于X轴的线段交OE于点H,四边形ODBE被分为梯形EBDH和△ODH这样便有S四边形ODBE=S梯形EBDH+S△ODH当然也可把补形与分割结合起来运用,即S四边形ODBE=S梯形OADH+S梯形HDCE。三.做法展示(一)补形法S四边形ODBE=S梯形OABC-S△AOD=(OA+BE)-OA.=〔5+(2-)〕6-×2×5=12(二)分割法由:y=x令y=2得到x=即H(,2)从而S四边形ODBE=S梯形EBDH+S△ODH=(DH+BE)(-)+DH.=(+)×4+××2=12四.方法总结对于直角坐标系中面积的算法,要牢牢抓住坐标轴或平行于坐标轴的线段用补形或分割来解决,无论是何种函数图象只要根据题意,把图形做适当地分割或补形都能够解决,当然有些时候要两种方法结合起来运用。五.牛刀小试(2014•兰州中考第28题)如图,抛物线y=﹣x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的表达式;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.