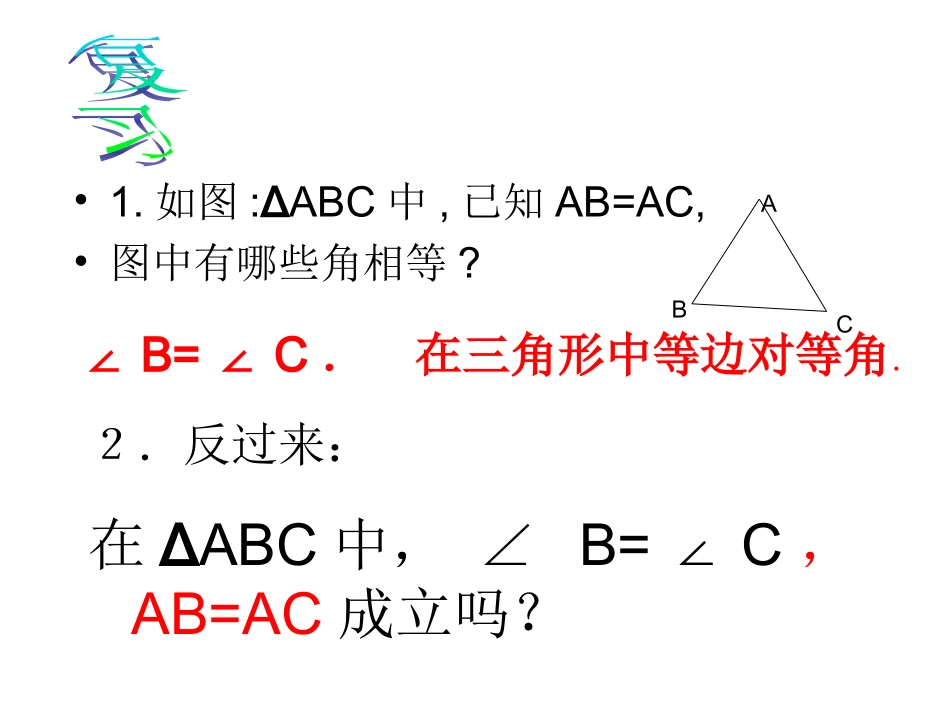
2.4等腰三角形的判定定理•1.如图:ΔABC中,已知AB=AC,•图中有哪些角相等?ABC∠B=C∠.在三角形中等边对等角.2.反过来:在ΔABC中,∠B=C∠,AB=AC成立吗?探索思考1,作一个三角形,有两个角相等,这两个角所对的边是否相等?ABC在ΔABC中,∠B=C∠作∠BAC的平分线交BC于D,则∠1=2∠,又∠B=C∠,由三角形内角和的性质得∠ADB=ADC∠,沿直线分析:AD折叠∠ADB=ADC∠,∠1=2∠,所以射线DB与射线DC重合,射线AB与射线AC重合,从而点B与点C重合,因此AB=ACD12等腰三角形有以下的判定方法:•如果一个三角形有两个角相等,那么这个三角形是等腰三角形.•简单地说;在同一个三角形中,•等角对等到边.定理的证明:等腰三角形的判定•如果一个三角形有两个角相等,那么这个三角形是等腰三角形.已知:如图,在△ABC中,B∠=∠C.求证:AB=AC.分析:要证明AB=AC,只要能构造出AB,AC所在的两个三角形全等就可以了.(同学们自已完成证明.)ABC•等边三角形在等腰三角形中,有一种特殊的情况,就是底边与腰相等,这时,三角形三边相等。我们把三条边都相等的三角形叫做等边三角形(正三角形)。•1.三个内角都等于60°的三角形是等边三角形.∵∠A=B=C=60°∠∠∴AB=AC=BC(为什么)∴三角形△ABC是等边三角形.等边三角形判定探索:ABCCA•2.有一个内角等于60°的等腰三角形是等边三角形.假若AB=AC,则∠B=C∠当顶角∠A=60°时,∠B=C=60∠°∴∠A=B=C=60∠∠°ABC∴△是等边三角形.当底角∠B=60时,∠C=60°,A=180—(60∠°+60°)=60.°∴∠A=B=C=60∠∠°ABC∴△是等边三角形.等边三角形性质探索:ABC等边三角形的判定方法:•1.三边相等的三角形是等边三角形.•2.三个内角都等于60°的三角形是等边三角形.•3.有一个内角等于60°的等腰三角形是等边三角形.如图,ABC△为等边三角形,1=2=3∠∠∠(1)求BEC的度数.(2)DEF△为等边三角形吗?为什么?ABCDFE312练习•例1.一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得C=30°.量出AC的长,它就是河宽(即A,B之间的距离).这个方法正确吗?请说明理由.•解:小聪的测量方法正确.理由如下:•∵∠DAC=∠B+∠C(三角形的外角的性质)•∴∠ABC=∠DAC-∠C=60°-30°=30°•∴∠ABC=∠C•∴AB=AC(在一个三角形中,等角对等边.)基本应用60°BACD上午10时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°,∠NBC=80°求从B处到灯塔C的距离NBAC80°40°北解:∵∠NBC=∠A+∠C∴∠C=80°-40°=40°∴BA=BC(等角对等边)∵AB=20(12-10)=40∴BC=40答:B处到达灯塔C40海里练习3基本应用例2.如果三角形一个角的外的角平分线平行于三角形的第三边,那么这个三角形是等腰三角形吗?为什么?ABCD12解:因为AD∥BC,所以∠1=∠B,∠2=∠C.因为∠1=∠2,∠B=∠C.因此AB=AC,即ΔABC的是等腰三角形.练习41.已知:如图,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?ABDC思考1:如图,在△ABC中,已知∠ABC=∠ACB,BF平分∠ABC,CF平分∠ACB,请想想看,由以上条件,你能推导出什么结论?并说明理由.ABCFEG如果EGBC∥?开启智慧与同伴交流你在探索思路的过程中的具体做法.ACBD●●E●●●●ACBMNACBPQ开启智慧下例各说法对吗?为什么?等腰三角形两底角的平分线相等.等腰三角形两腰上的中线相等.等腰三角形两腰上的高相等.思考2: