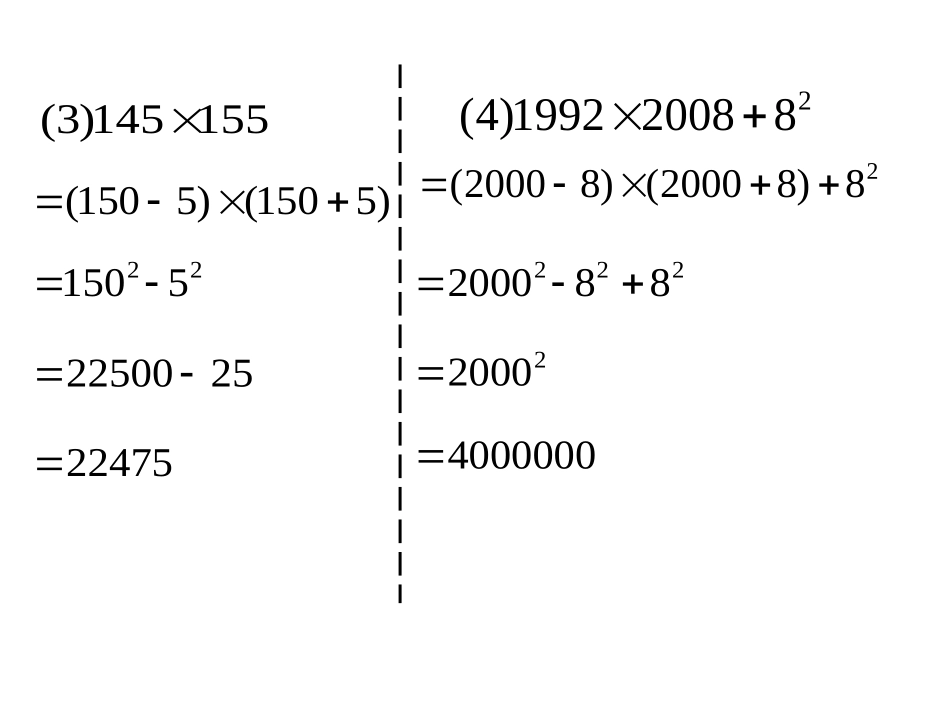平方差公式 课件VIP免费

(a(a++b)(ab)(a--b)=ab)=a22--bb22左边两个数的和乘以这两个数的差。右边这两数的平方差。即两个二项式中有两项相等，另两项是互为相反数。即相等数的平方减去互为相反数的数的平方。注意：注意：公式中的公式中的aa，，bb既可代表单项式，还可代表具体既可代表单项式，还可代表具体的数或多项式。的数或多项式。复习平方差公式一、用平方差公式计算:97103)1(122118)2(155145)3(2820081992)4(97103)1(:解)3100()3100(2231009991122118)2()2120()2120(22212014396910000414400155145)3()5150()5150(22515022475252250028)82000()82000(2228820004000000220002820081992)4(二、运用平方差公式计算222))(()1(bababaa)31)(31()1()3(xxxx(2)(2x-5)(2x+5)-2x(2x-3)222ba)ba)(ba(a)1(:解22222ba)ba(a22224babaa4a(2)(2x-5)(2x+5)-2x(2x-3)=(2x)2-(5)2-(2x)2+6x=-25+6x=6x-25)31)(31()1()3(xxxx])31(x[)xx(2222)31(xxx2291x三、综合运用平方差公式4902898)2(172174173)3(2)1x4)(1x2)(1x2)(1(2)1x4)(1x2)(1x2)(1(:2解)1x4](1)x2[(222)1x4)(1x4(221x1624902898)2(4)2900()2900(4)2900(2244810000810000172174173)3(2)1173()1173(1732)1173(173222222117317311)(a+b+c)(a+b-c)=()-()22223)(a+b-c+d)(a-b-c-d)=()-()222)(x-y-z)(x+y+z)=()-()a+bCxy+za-cb+d四、填空补充:(1)(y+2)(y-2)-(3-y)(3+y)(2)(3m-4n)(4n+3m)-(2m-n)(2m+3n)在整式的乘法运算中，只有符合公式要求的乘法，才能运用公式简化运算，其余的运算仍按乘法法则进行。评：补充2计算:的值2219981999注意公式的逆用。评：解：原式=（1999+1998)(1999-1998)=3997×1=3997五、思考题1)12()12()12)(12)(12(32421.王红同学在计算（2+1)(22+1)(24+1)时，将积式乘以（2-1）得：解：原式=(2-1)(2+1)(22+1)(24+1)=(22-1)(22+1)(24+1)=(24-1)(24+1)=28-1你能根据上题计算:(2+1)(22+1)(24+1)(28+1)(216+1)的结果吗？)41)(21)(21(2xxx1.2.(2+1)(4+1)(16+1)(256+1))116)(14)(12)(12(222(2-1)(2+1)(4+1)(16+1)(256+1)可连续使用平方差公式得出题目的解分析：分析：引申