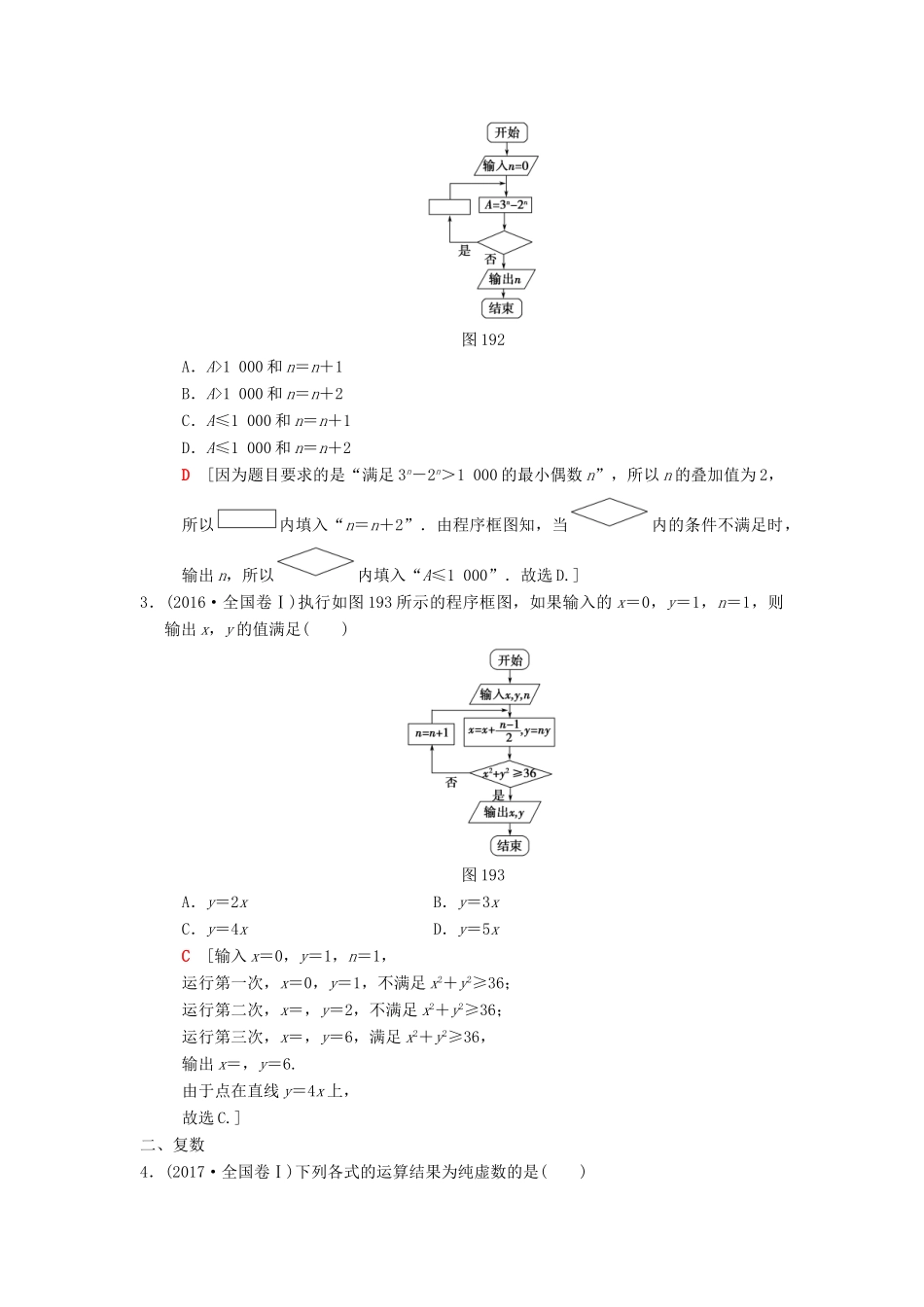
专题限时集训(十九)算法初步、复数、推理与证明[建议A、B组各用时:45分钟][A组高考题、模拟题重组练]一、程序框图(流程图)1.(2017·全国卷Ⅲ)执行如图191所示的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为()图191A.5B.4C.3D.2D[假设N=2,程序执行过程如下:t=1,M=100,S=0,1≤2,S=0+100=100,M=-=-10,t=2,2≤2,S=100-10=90,M=-=1,t=3,3>2,输出S=90<91.符合题意.∴N=2成立.显然2是N的最小值.故选D.]2.(2017·全国卷Ⅰ)如图192所示的程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在和两个空白框中,可以分别填入()图192A.A>1000和n=n+1B.A>1000和n=n+2C.A≤1000和n=n+1D.A≤1000和n=n+2D[因为题目要求的是“满足3n-2n>1000的最小偶数n”,所以n的叠加值为2,所以内填入“n=n+2”.由程序框图知,当内的条件不满足时,输出n,所以内填入“A≤1000”.故选D.]3.(2016·全国卷Ⅰ)执行如图193所示的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足()图193A.y=2xB.y=3xC.y=4xD.y=5xC[输入x=0,y=1,n=1,运行第一次,x=0,y=1,不满足x2+y2≥36;运行第二次,x=,y=2,不满足x2+y2≥36;运行第三次,x=,y=6,满足x2+y2≥36,输出x=,y=6.由于点在直线y=4x上,故选C.]二、复数4.(2017·全国卷Ⅰ)下列各式的运算结果为纯虚数的是()A.i(1+i)2B.i2(1-i)C.(1+i)2D.i(1+i)C[A项,i(1+i)2=i(1+2i+i2)=i×2i=-2,不是纯虚数.B项,i2(1-i)=-(1-i)=-1+i,不是纯虚数.C项,(1+i)2=1+2i+i2=2i,是纯虚数.D项,i(1+i)=i+i2=-1+i,不是纯虚数.故选C.]5.若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是()A.(-∞,1)B.(-∞,-1)C.(1,+∞)D.(-1,+∞)B[ (1-i)(a+i)=a+i-ai-i2=a+1+(1-a)i,又 复数(1-i)(a+i)在复平面内对应的点在第二象限,∴解得a<-1.故选B.]6.(2016·全国卷Ⅰ)设(1+i)x=1+yi,其中x,y是实数,则|x+yi|=()A.1B.C.D.2B[ (1+i)x=1+yi,∴x+xi=1+yi.又 x,y∈R,∴x=1,y=x=1.∴|x+yi|=|1+i|=,故选B.]7.(2016·全国卷Ⅲ)若z=4+3i,则=()A.1B.-1C.+iD.-iD[ z=4+3i,∴=4-3i,|z|==5,∴==-i.]8.(2015·全国卷Ⅰ)设复数z满足=i,则|z|=()A.1B.C.D.2A[由=i,得z====i,所以|z|=|i|=1,故选A.]三、合情推理9.(2017·全国卷Ⅱ)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则()A.乙可以知道四人的成绩B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩D[由甲说:“我还是不知道我的成绩”可推知甲看到乙、丙的成绩为“1个优秀、1个良好”.乙看丙的成绩,结合甲的说法,丙为“优秀”时,乙为“良好”;丙为“良好”时,乙为“优秀”,可得乙可以知道自己的成绩.丁看甲的成绩,结合甲的说法,甲为“优秀”时,丁为“良好”;甲为“良好”时,丁为“优秀”,可得丁可以知道自己的成绩.故选D.]10.(2016·全国卷Ⅱ)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.1和3[法一:由题意得丙的卡片上的数字不是2和3.若丙的卡片上的数字是1和2,则由乙的说法知乙的卡片上的数字是2和3,则甲的卡片上的数字是1和3,满足题意;若丙的卡片上的数字是1和3,则由乙的说法知乙的卡片上的数字是2和3,则甲的卡片上的数字是1和2,不满足甲的说法.故甲的卡片上的数字是1和3.法二:因为甲与乙的卡片上相同的数字不是2,所以丙的卡片上必有数字2.又丙的卡片上的数字之和不是5,所以丙的卡片上的数字是1和2.因为乙与丙的...