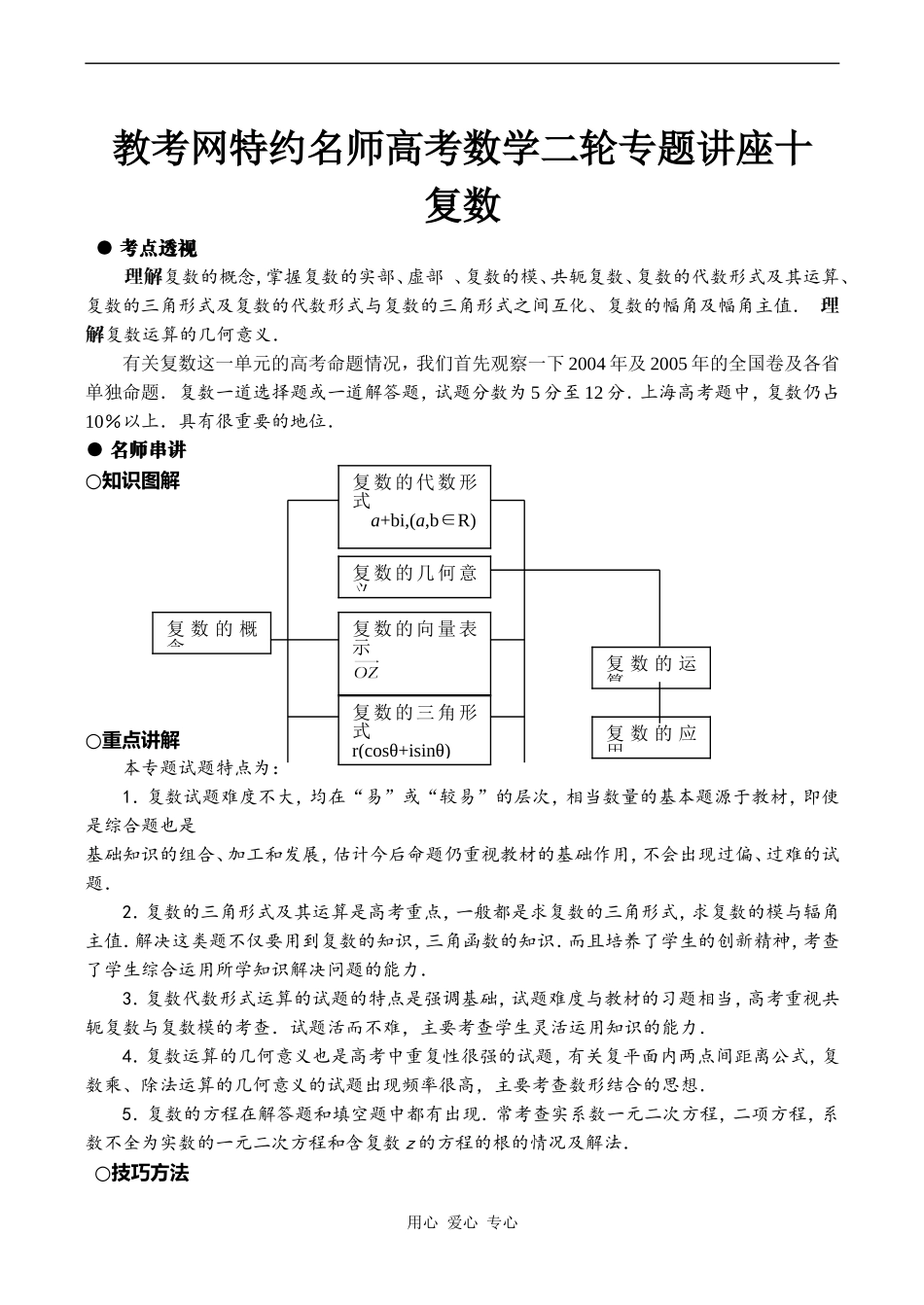
教考网特约名师高考数学二轮专题讲座十复数●考点透视理解复数的概念,掌握复数的实部、虚部、复数的模、共轭复数、复数的代数形式及其运算、复数的三角形式及复数的代数形式与复数的三角形式之间互化、复数的幅角及幅角主值.理解复数运算的几何意义.有关复数这一单元的高考命题情况,我们首先观察一下2004年及2005年的全国卷及各省单独命题.复数一道选择题或一道解答题,试题分数为5分至12分.上海高考题中,复数仍占10%以上.具有很重要的地位.●名师串讲○知识图解○重点讲解本专题试题特点为:1.复数试题难度不大,均在“易”或“较易”的层次,相当数量的基本题源于教材,即使是综合题也是基础知识的组合、加工和发展,估计今后命题仍重视教材的基础作用,不会出现过偏、过难的试题.2.复数的三角形式及其运算是高考重点,一般都是求复数的三角形式,求复数的模与辐角主值.解决这类题不仅要用到复数的知识,三角函数的知识.而且培养了学生的创新精神,考查了学生综合运用所学知识解决问题的能力.3.复数代数形式运算的试题的特点是强调基础,试题难度与教材的习题相当,高考重视共轭复数与复数模的考查.试题活而不难,主要考查学生灵活运用知识的能力.4.复数运算的几何意义也是高考中重复性很强的试题,有关复平面内两点间距离公式,复数乘、除法运算的几何意义的试题出现频率很高,主要考查数形结合的思想.5.复数的方程在解答题和填空题中都有出现.常考查实系数一元二次方程,二项方程,系数不全为实数的一元二次方程和含复数z的方程的根的情况及解法.○技巧方法用心爱心专心复数的概念复数的几何意义复数的代数形式a+bi,(a,b∈R)复数的三角形式r(cosθ+isinθ)复数的向量表示复数的运算复数的应用对2006年高考命题趋势的预测,根据2003年、2004年、2005年高考命题情况,以及新教材的逐渐普及使用,预计2006年全国高考对复数试题的考查要求仍然很低,不会出现偏难题,估计还以课本的习题改编成的选择题形式命题,重在考查基本概念和基本运算.●考题解析【例1】(2004年上海卷)已知复数z1满足(1+i)z1=-1+5i,z2=a-2-i,其中i为虚数单位,a∈R,若<,求a的取值范围.【思路串讲】本题主要考查复数的运算、模、共轭复数等基本知识,以及解方程、解不等式的基本方法和计算技能.作为解答题的第一个题目,贴近课本,利于稳定考生的应试心理.本题考查的知识点较多,由于选拔性考试本身决定了试题不能只局限于课本的要求,即使是起始题,也必须考查一定的知识容量和综合运用知识解决问题的能力.本题巧妙地将复数的代数形式、运算、模、共轭复数和解方程、解不等式等融合于一体,但解题思路都是常规的,对考生解答后面的大题,奠定了心理基础.解题突破口:复数有两种表示形式,即代数形式和三角形式;复数几何意义有两种表达方式,即复平面内的点和向量.由于复数的表示形式和几何意义的一些不同,因而复数问题的解题策略总种上有三种:实数化、三角化、图形化.本题应用三角化显然不方便,故可采用实数化和图形化来处理.【标准答案】由题意得z1==2+3i,于是==,=.<,得a2-8a+7<0,1