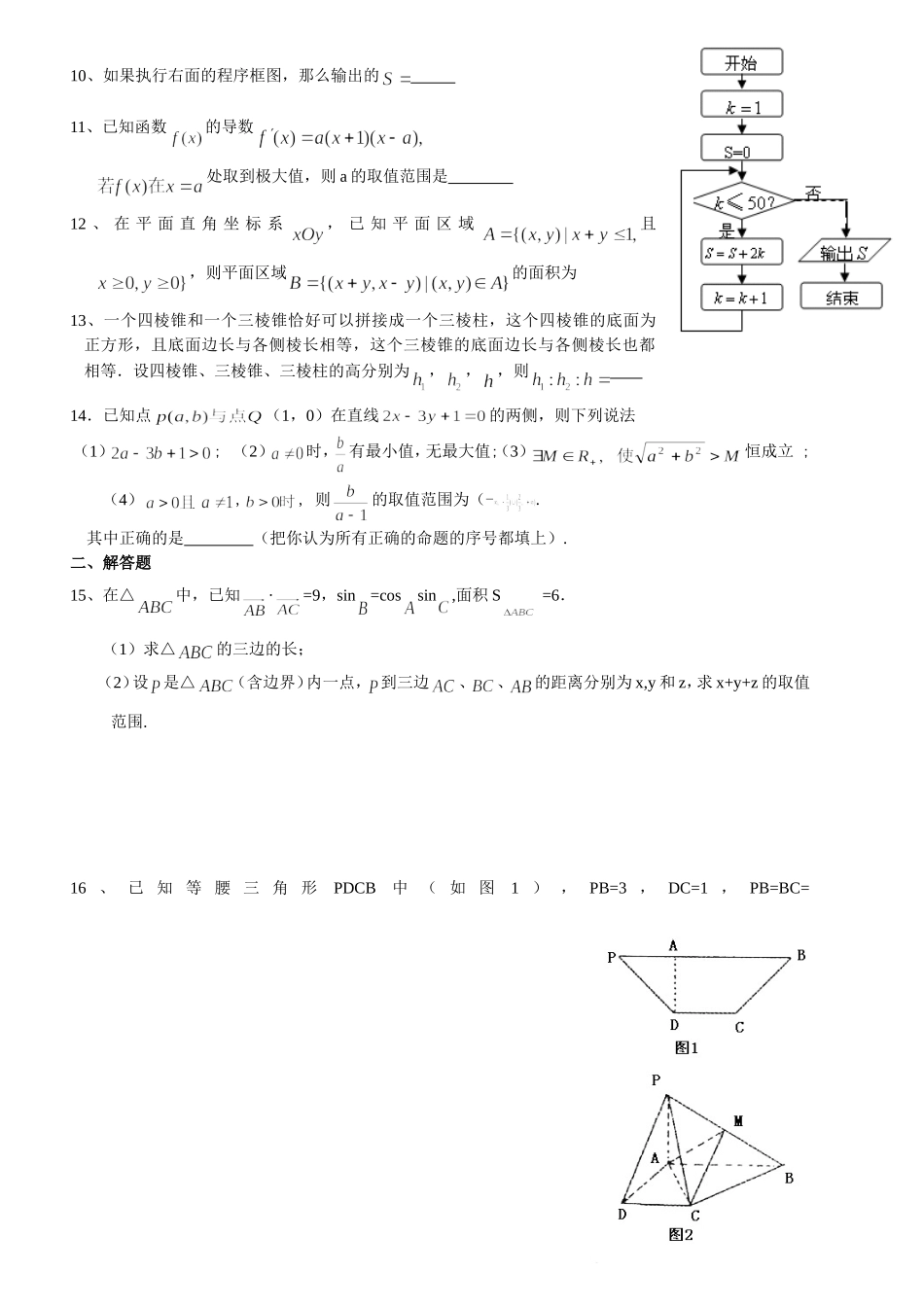
如东县教研室高三上学期期末考试调研试卷说明:本试卷满分160分,考试时间120分钟。一、填空题:本大题共14小题,每小题5分,共70分.答案填在题中横线上1、复数在复平面上对应的点位于第__象限.2、曲线在点处的切线与坐标轴所围三角形的面积为3、在△ABC中,BC=1,,当△ABC的面积等于时,__4、给出下列关于互不相同的直线和平面的四个命题:(1)则与m不共面;(2)、m是异面直线,;(3)若,则(4)若其中真命题是(填序号)5、一枚半径为1的硬币随机落在边长为3的正方形所在平面内,且硬币一定落在正方形内部或与正方形有公共点,则硬币与正方形没有公共点的概率是6、甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表分别表示甲、乙、丙三人成绩的标准差,则的大小顺序是7、某医疗研究所为了检验某种血清预防感冒的作用,把名使用血清的人与另外名未用血清的人一年中的感冒记录作比较,提出假设:“这种血清不能起到预防感冒的作用”,利用列联表计算得,经查对临界值表知.则下列结论中,正确结论的序号是(1)有的把握认为“这种血清能起到预防感冒的作用”(2)若某人未使用该血清,那么他在一年中有的可能性得感冒(3)这种血清预防感冒的有效率为(4)这种血清预防感冒的有效率为8、设,分别为具有公共焦点与的椭圆和双曲线的离心率,为两曲线的一个公共点,且满足,则的值为9、设是等差数列的前项和,若以点为顶点的四边形(其中)中,则之间的等量关系式经化简后为.甲的成绩环数78910频数5555乙的成绩环数78910频数6446丙的成绩环数78910频数466410、如果执行右面的程序框图,那么输出的11、已知函数的导数处取到极大值,则a的取值范围是12、在平面直角坐标系,已知平面区域且,则平面区域的面积为13、一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为,,,则14.已知点(1,0)在直线的两侧,则下列说法(1);(2)时,有最小值,无最大值;(3)恒成立;(4),,则的取值范围为(-.其中正确的是(把你认为所有正确的命题的序号都填上).二、解答题15、在△中,已知·=9,sin=cossin,面积S=6.(1)求△的三边的长;(2)设是△(含边界)内一点,到三边、、的距离分别为x,y和z,求x+y+z的取值范围.16、已知等腰三角形PDCB中(如图1),PB=3,DC=1,PB=BC=FOAPQyx,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2).(1)证明:平面PAD⊥平面PCD;(2)试在棱PB上确定一点M,使截面AMC把几何体分成的两部分;17、有序实数对,记A为事件。已知计算机随机产生的有序实数对满足,通过计算可得。现在若用连续抛骰子两次分别得到的有序实数对,求18、设椭圆C:的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且.⑴求椭圆C的离心率;⑵若过A、Q、F三点的圆恰好与直线l:相切,求椭圆C的方程.19、已知函数有下列性质:“若使得”成立,(1)利用这个性质证明唯一.(2)设A、B、C是函数图象上三个不同的点,求证:△ABC是钝角三角形.20、如果有穷数列(为正整数)满足条件,,…,,即(),我们称其为“对称数列”.例如,由组合数组成的数列就是“对称数列”.(1)设是项数为7的“对称数列”,其中是等差数列,且,.依次写出的每一项;(2)设是项数为(正整数)的“对称数列”,其中是首项为,公差为的等差数列.记各项的和为.当为何值时,取得最大值?并求出的最大值;(3)对于确定的正整数,写出所有项数不超过的“对称数列”,使得依次是该数列中连续的项;当时,求其中一个“对称数列”前项的和.参考答案一、填空题1、三2、3、4、(1)、(2)、(3)5、6、7、(1)8、29、10、255011、(0,+)12、213、14、(3)(4)二、解答题15、解:设(1),,,,,由,用余弦定理得(2)设,由线性规划得∴16、解:(1)证明:依题意知:(2)由(I)知平面ABCD∴平面PAB⊥平面ABCD.在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,设MN=h则要使即M为PB的中点.17、18、...