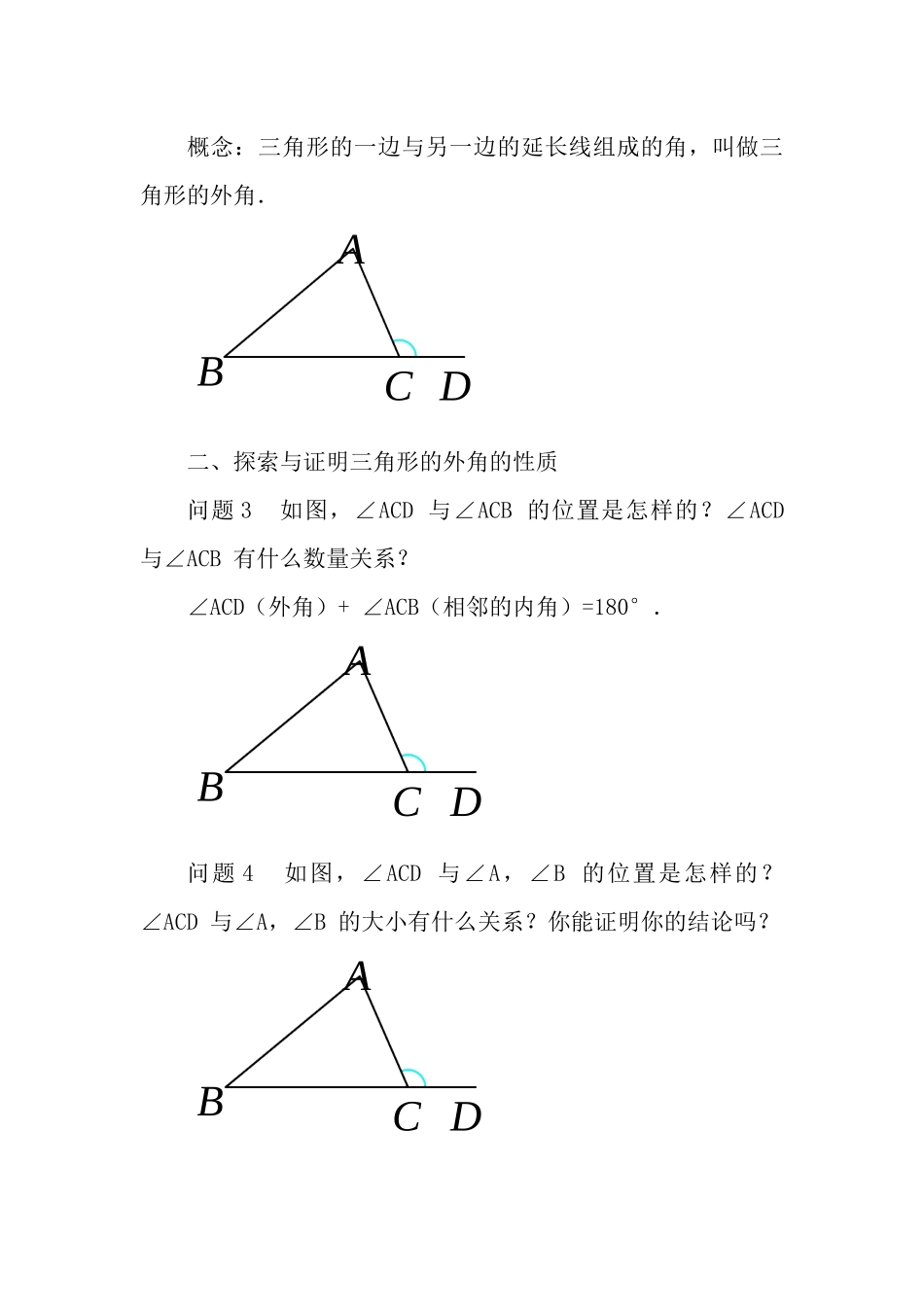
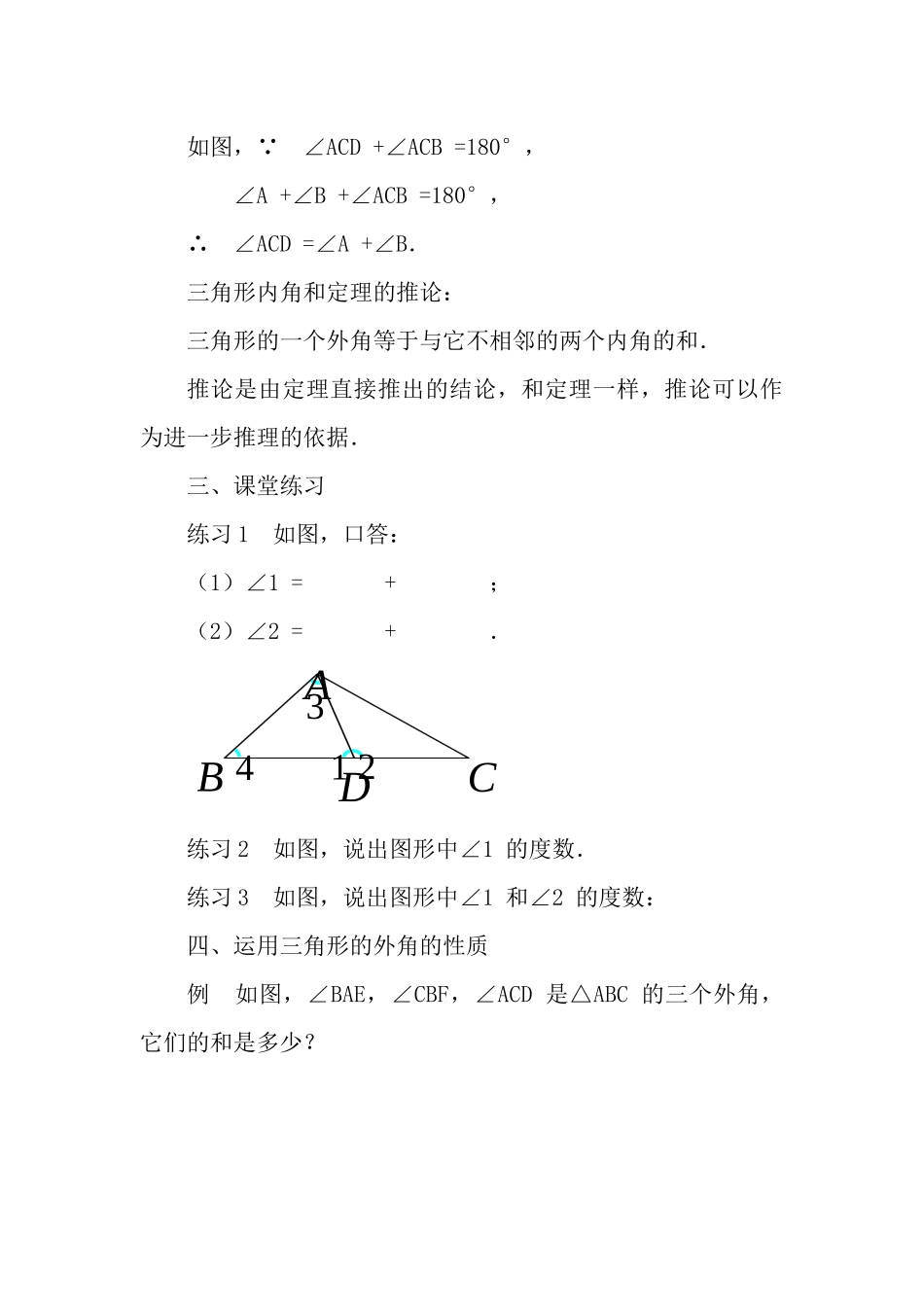
三角形的外角教案教学目标:1、知识目标:①了解三角形的外角;②探索并了解三角形的一个外角等于与它不相邻的两个内角的和;2、能力目标:①学会运用简单的说理来计算三角形相关的角;②培养学生的实践能力和观察总结能力,体验主动探究的成功和快乐.3、情感目标:①让学生在探索活动中产生对数学的好奇心,发展学生的空间观念;②体验探索的乐趣和成功的快乐,增强学好数学的信心。教学重点:三角形的外角性质。教学难点:运用三角形外角性质进行有关计算能准确地表达推理的过程和方法。教学过程:一、理解三角形的外角的概念问题1在△ABC中,∠A=75°,∠B=40°,∠C等于多少度?问题2如图,把△ABC的一边BC延长,得到∠ACD.这个角还是三角形的内角吗?概念:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.二、探索与证明三角形的外角的性质问题3如图,∠ACD与∠ACB的位置是怎样的?∠ACD与∠ACB有什么数量关系?∠ACD(外角)+∠ACB(相邻的内角)=180°.问题4如图,∠ACD与∠A,∠B的位置是怎样的?∠ACD与∠A,∠B的大小有什么关系?你能证明你的结论吗?ABCDABCDABCD如图,∵∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,∴∠ACD=∠A+∠B.三角形内角和定理的推论:三角形的一个外角等于与它不相邻的两个内角的和.推论是由定理直接推出的结论,和定理一样,推论可以作为进一步推理的依据.三、课堂练习练习1如图,口答:(1)∠1=+;(2)∠2=+.练习2如图,说出图形中∠1的度数.练习3如图,说出图形中∠1和∠2的度数:四、运用三角形的外角的性质例如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?BACD1234解法一:∵∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2,∴∠BAE+∠CBF+∠ACD=(∠2+∠3)+(∠1+∠3)+(∠1+∠2)=2(∠1+∠2+∠3).∵∠1+∠2+∠3=180°,∴∠BAE+∠CBF+∠ACD=2×180°=360°.解法二:由∠1+∠BAE=180°,∠2+∠CBF=180°,∠3+∠ACD=180°,得∠1+∠2+∠3+∠BAE+∠CBF+∠ACD=540°.由∠1+∠2+∠3=180°,得∠BAE+∠CBF+∠ACD=540°-180°=360°.ABFCDE123五、课堂练习练习如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:(1)∠B的度数;(2)∠C的度数.六、课堂小结(1)本节课学习了哪些主要内容?(2)怎样探索并证明“三角形的一个外角等于与它不相邻的两个内角的和”?(3)你用了哪几种方法解答例题?七、布置作业教科书习题11.2第6、8题.八、板书设计三角形的外角三角形的外角概念三角形的外角性质三角形的外角(八年级上册)学校:白杨沟镇中心学校教师:吕慧