高中数学向量加法运算及其几何意义课件VIP免费

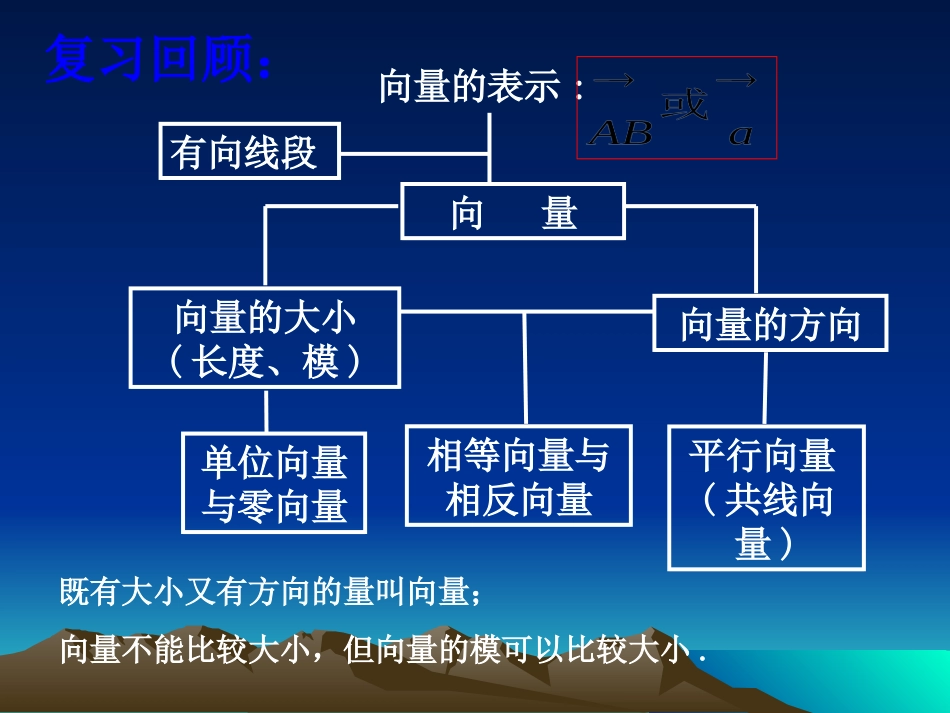
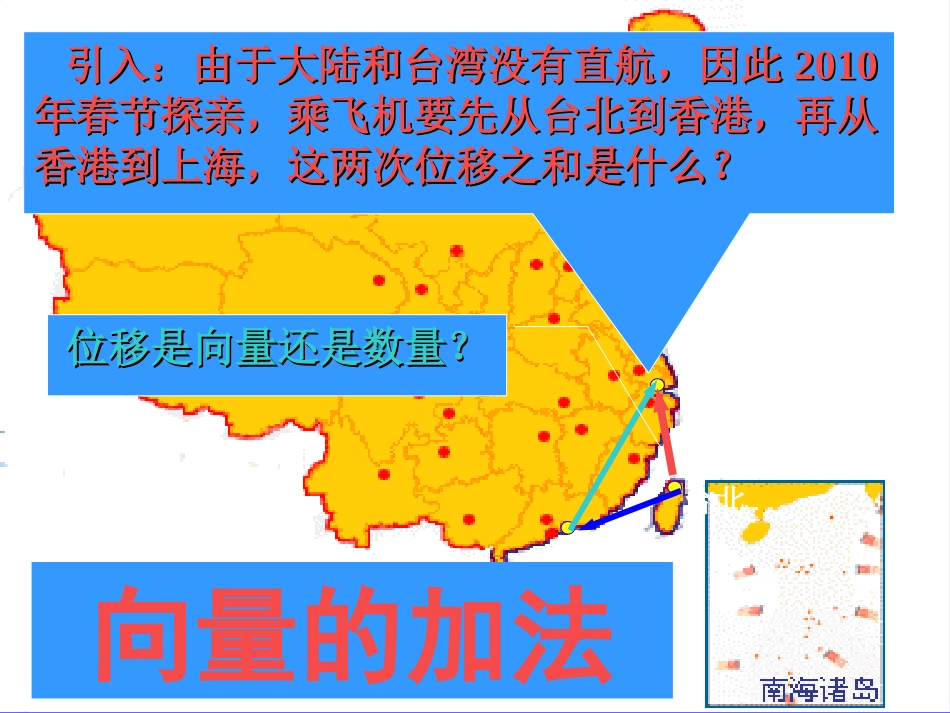
相等向量与相反向量复习回顾：单位向量与零向量向量向量的大小(长度、模)向量的方向有向线段平行向量(共线向量)既有大小又有方向的量叫向量；向量不能比较大小，但向量的模可以比较大小.向量的表示:台北香港上海引入：由于大陆和台湾没有直航，因此引入：由于大陆和台湾没有直航，因此20102010年春节探亲，乘飞机要先从台北到香港，再从年春节探亲，乘飞机要先从台北到香港，再从香港到上海，这两次位移之和是什么？香港到上海，这两次位移之和是什么？位移是向量还是数量？位移是向量还是数量？向量的加法F1F2FEOOE例如:橡皮条在力F1与F2的作用下,从E点伸长到了O点.同时橡皮条在力F的作用下也从E点伸长到了O点.问:合力F与力F1、F2有怎样的关系？F1+F2=F力F对橡皮条产生的效果，与力F1和F2共同作用产生的效果相同，物理学中把力F叫做F1和F2的合力.上述事例表明，两个向量可以相加，并且两个向量的和还是一个向量.一般地，求两个向量和的运算，叫做向量的加法.AC2.它们之们有联系吗?1.两种方法做出的结果一样吗?向量加法的定义任意给出两个向量a与b.ababBa+babBOACa+bACBCABbbaba三角形法则:平行四边形法则:AC2.它们之们有联系吗?1.两种方法做出的结果一样吗?向量加法的定义任意给出两个向量a与b.ababBa+babBOACa+bb位移的合成可以看作向量加法三角形法则的物理模型.力的合成可以看作向量加法平行四边形法则的物理模型.向量加法的三角形法则:1.将向量平移使得它们首尾相连方法巩固:2.和向量即是第一个向量的首指向第二个向量的尾向量加法的平行四边形法则:1.将向量平移到同一起点2.和向量即以它们作为邻边平行四边形的共起点的对角线ababa+bbaa+b,00aaaa对于零向量与任一向量我们规定特例：共线向量abABC方向相同abCAB方向相反baACbaAC问题：除了零向量，有没有不能用平行四边形法则求和向量的情况？____,abab(<,>,,)请选用合适符号连接：,ab非零向量处于什么位置时？(1)(2)(3)(4)abababababababbaab，不共线或共线反向ab，共线且同向abab，反向且abab，反向且探究探究ADDE�PMMC�CFFG�ABAO�ABEB�AB�AE�PC�CG�OB�AE�AD�DB�练习2：用适当的向量填空：问题探究问题探究运算律可以帮助我们有效地简化运算实数的加法运算满足交换律，即对任意a，bR∈，都有a＋b=b＋a.那么向量的加法也满足交换律吗？如何检验？ba+babaabcabcABCDABCDa+b(a+b)+ca+(b+c)b+c实数的加法运算满足结合律，即对任意a，b，cR∈，都有（a＋b）＋c=a＋（b＋c）.那么向量的加法也满足结合律吗？如何检验？问题探究问题探究abba()abcabc(+)+向量加法满足交换律和结合律(1)向量加法交换律：(2)向量加法结合律：以上两个运算律可以推广到任意多个向量.例１.化简________)1(BCCDAB________)2(CBACBNMA(3)_____ABBDCADC�学以致用ADMN0例2.长江两岸之间没有大桥的地方，常常通过轮船进行运输，如图所示，一艘船从长江南岸A点出发，以km/h的速度向垂直于对岸的方向行驶，同时江水的速度为向东2km/h.（1）试用向量表示江水速度、船速以及船实际航行的速度；（2）求船实际航行的速度的大小与方向（用与江水速度的夹角来表示）。23(2)||2,||23RtABCABBC�解：在中，2222||||||2(23)4ACABBC�23tan32CAB60.CAB答：船实际航行速度为4km/h,方向与水的流速间的夹角为60º。ADBC若水流速度和船速的大小保持不变,最后要能使渡船垂直过江,则船的航向应该如何?并作图探究.探究DC2BA3210103akmbkmab1.若表示“向南走”，表示“向西走”，则表示________.练习题2.35ababababab若，满足，，求的最大值，并指出，满足什么条件时?取到最大值.课堂小结：课堂小结：向量加法的物理背景向量的加法运算向量加法的运算律平行四边形法则平行四边形法则三角形法则向量加法实际应用作业:1.复习向量的加法知识；2.预习课本P85-86；3.作业:课本P91A组2，3，4