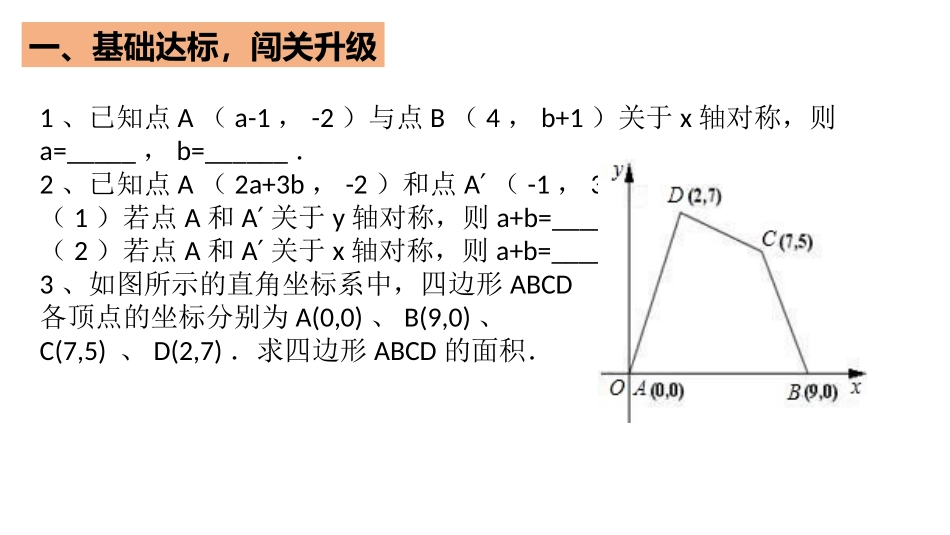
【学习目标】熟练掌握平面直角坐标系的相关知识,会根据坐标求复杂图形的面积。【重点】在做题的过程中有数形结合的思想。1、已知点A(a-1,-2)与点B(4,b+1)关于x轴对称,则a=_____,b=______.2、已知点A(2a+3b,-2)和点A′(-1,3a+b).(1)若点A和A′关于y轴对称,则a+b=______;(2)若点A和A′关于x轴对称,则a+b=______.3、如图所示的直角坐标系中,四边形ABCD各顶点的坐标分别为A(0,0)、B(9,0)、C(7,5)、D(2,7).求四边形ABCD的面积.一、基础达标,闯关升级过D,C分别作DE,CF垂直于AB,E、F分别为垂足,则有:S=SOED△+SEFCD+SCFB△1.已知平行四边形ABCD中,A、B、C三点的坐标分别是(-1,-1),(5,-1),(3,5),求顶点D的坐标.解:∵ABCD是平行四边形,且已知A(-1,-1),B(5,-1),C(3,5).∴当ABCD∥,ADBC∥时,D点坐标为________________________当ABCD∥,ACBD∥时,D点坐标为________________________当ADCB∥,ACDB∥是,D点坐标为________________________综上,顶点D的坐标为________________________二、例题精讲(-3,5),(9,5)或(1,-7)2.已知:A(0,1),B(2,0),C(4,3)(1)求△ABC的面积;(2)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.二、例题精讲解:(1)=4;(2)P1(-6,0)、P2(10,0)、P3(0,5)、P4(0,-3).1、坐标平面内有点A(4,8),B(-4,-8),以坐标轴为对称轴,点A可以由点B经过m次轴对称变换得到,则m的最小值为.三、能力提升,发散思维∵点A(4,8),B(-4,-8),∴点A与B关于原点对称,∴先作出点A关于x轴的对称点C之后,再作出点C关于y轴的对称点,即为点B;或者先作出点A关于y轴的对称点D之后,再作出点D关于x轴的对称点,即为点B.∴点A可以由点B经过2次轴对称变换得到,即m的最小值为2.2、(1)在平面直角坐标系中,如图1,将线段AB平移至线段CD,连接AC、BD。①直接写出图中相等的线段、平行的线段;②已知A(-3,0)、B(-2,-2),C(0,5),点D在第一象限内,点D的坐标______;三、能力提升,发散思维xyDBAoC(2)在平面直角坐标系中,如图,已知一定点M(1,0),两个动点E(a,2a+1)、F(b,-2b+3),请你探索是否存在以两个动点E、F为端点的线段EF平行于线段OM且等于线段OM。若存在,求以点O、M、E、F为顶点的四边形的面积,若不存在,请说明理由。xyoM