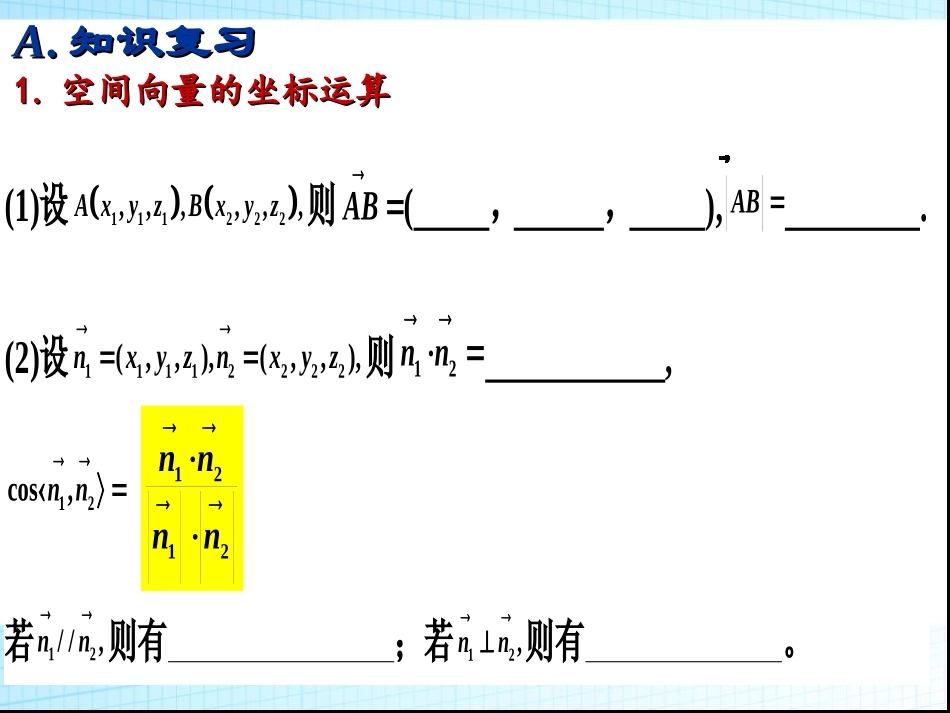
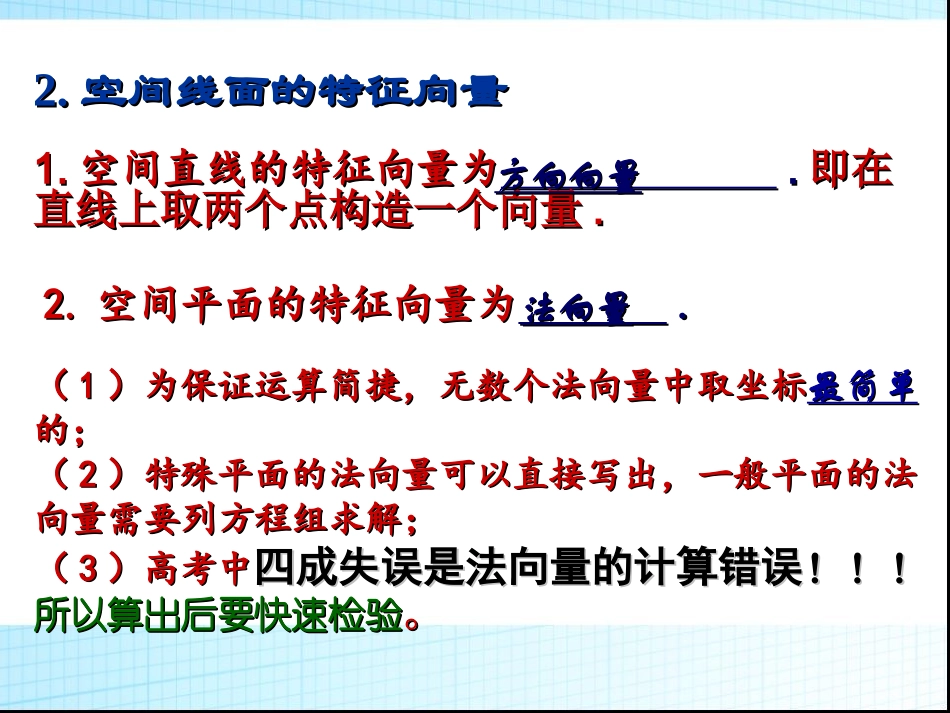
立体几何中的向量方法立体几何中的向量方法AA..知识复习知识复习1.1.空间向量的坐标运算空间向量的坐标运算(1)设111222,,,,,,AxyzBxyz则AB(,,),AB�.(2)设11112222(,,),(,,),nxyznxyz则12nn,12cos,nn.若12//,nn则有;若12,nn则有。2121nnnn2.2.空间线面的特征向量空间线面的特征向量1.1.空间直线的特征向量为空间直线的特征向量为..即在即在直线上取两个点构造一个向量直线上取两个点构造一个向量..2.2.空间平面的特征向量为空间平面的特征向量为..方向向量方向向量法向量法向量((11)为保证运算简捷,无数个法向量中取坐标)为保证运算简捷,无数个法向量中取坐标最简单最简单的;的;((22)特殊平面的法向量可以直接写出,一般平面的法)特殊平面的法向量可以直接写出,一般平面的法向量需要列方程组求解;向量需要列方程组求解;((33)高考中)高考中四成失误是法向量的计算错误四成失误是法向量的计算错误!!!!!!所以算出后要快速检验所以算出后要快速检验。。BB..新知学习新知学习立体几何主要研究的是立体几何主要研究的是•1.1.空间空间平行、垂直平行、垂直关系的证明关系的证明•2.2.空间空间夹角夹角(线线角、线面角、面面角)的计算(线线角、线面角、面面角)的计算•3.3.空间空间距离距离的计算的计算1.1.空间平行、垂直关系的证明空间平行、垂直关系的证明•直接转化为求证相应直线的方向向量及平面的直接转化为求证相应直线的方向向量及平面的法向量之间的关系法向量之间的关系则则ll⊥⊥mlml⊥⊥αααα⊥⊥ββll////mlml////αααα////ββ设直线l、m的方向向量分别为11112222(,,)(,,)nxyznxyz、;平面、的法向量分别为33334444(,,)(,,)nxyznxyz、,;21nn;31//nn;43nn;21//nn;31nn;43//nn2.2.空间夹角(线线角、线面角、面面角)的计空间夹角(线线角、线面角、面面角)的计算算设直线12ll、的方向向量分别为11112222(,,)(,,)nxyznxyz、;①则直线1l与2l直线的夹角1(即线线角)满足1cos;21,cosnn绝对值的作用:绝对值的作用:修正角的范围修正角的范围2.2.空间夹角(线线角、空间夹角(线线角、线面角线面角、面面角)的计、面面角)的计算算设直线l的方向向量为),,(1111zyxn平面的法向量为),,(3333zyxn,直线1l与平面所成的角2(即线面角)满足213sincos=,nn;1.绝对值的作用:绝对值的作用:修正角的范围修正角的范围2.2.角的名称发生了变化!角的名称发生了变化!2.2.空间夹角(线线角、线面角、空间夹角(线线角、线面角、面面角面面角)的计)的计算算平面、的法向量分别为33334444(,,)(,,)nxyznxyz、,③平面与平面所成的角(即二面角)3满足334coscos,=nn(取正负号唯一:锐二面角取正号,钝二面角取负号);解题时需先判断锐、钝角解题时需先判断锐、钝角2.2.空间夹角(线线角、线面角、面面角)的计空间夹角(线线角、线面角、面面角)的计算算设直线12ll、的方向向量分别为11112222(,,)(,,)nxyznxyz、;平面、的法向量分别为33334444(,,)(,,)nxyznxyz、,①则直线1l与2l直线的夹角1满足112coscos=,nn…;②直线1l与平面所成的角2满足213sincos=,nn…;③平面与平面所成的二面角3满足334coscos,=nn…①则直线1l与2l直线的夹角1满足112coscos=,nn…;②直线1l与平面所成的角2满足213sincos=,nn…;③平面与平面所成的二面角3满足334coscos,=nn…思考:思考:公式有公式有何规律何规律??构成要素构成要素同同则则余弦余弦,,异异则则正弦正弦3.3.空间点到平面的距空间点到平面的距离离点P到平面α的距离d满足33si.nPQndOPPQn设设PP、、QQ分别为平面分别为平面αα外、内一点,且平面外、内一点,且平面αα的法向量为的法向量为,则,则3n公式中分母是公式中分...