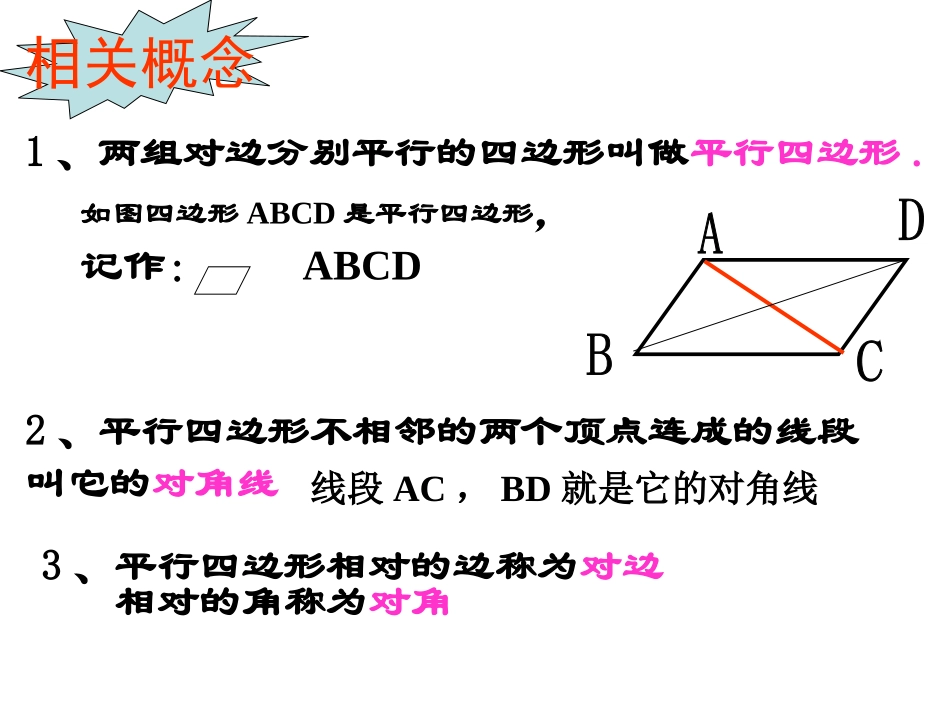
平行四边形的性质(1)活动1看下列图片,你能找到什么图形?再从生活中找一找。1、两组对边分别平行的四边形叫做平行四边形.相关概念如图四边形ABCD是平行四边形,记作:ABCD2、平行四边形不相邻的两个顶点连成的线段叫它的对角线线段AC,BD就是它的对角线3、平行四边形相对的边称为对边相对的角称为对角第十九章四边形活动2取两个全等的三角形纸片,将它们相等的一边重合,拼出一个平行四边形。你拼出了怎样的平行四边形?小组内交流从拼图可以得到什么启示?从拼图可以得到什么启示?小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。想一想:由定义可以得出平行四边形的什么性质?ABCD平行四边形的两组对边分别平行根据定义在方格纸中画一个平行四边形,观察这个四边形,除了“两组对边分别平行”以外,它的边与边、角与角之间有什么关系吗?度量一下,是不是和你们的猜想一致?小组内交流得出的结论。ABCD方法1:活动3还有别的方法验证吗CBAD结论:平行四边形的对边相等方法2:平移方法3:旋转ABCDO结论:平行四边形的对角相等。思考:平行四边形中相邻的两角有什么关系呢?互补ABCD平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互补平行四边形的性质如何证明前两条结论?已知:ABCD(如图)求证:AB=CD,BC=DA;∠B=D∠,∠BAD=D∠CB即∠BAD=∠DCB证明:连结AC∵ABCD∥,ADBC∥(平行四边形的定义)∴∠1=∠2,∠3=∠4∴ABCCDA≌(ASA)∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3ABCD1234∵AC=CA解:∵四边形ABCD是平行四边形∴AB=CD,AD=BC∵AB=8m∴CD=8m又AB+BC+CD+AD=36,∴AD=BC=10mABCD例1如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长8m,其他三边的长各是多少?运用所学知识解决问题尝试应用1、如图,ABCD中,∠B=50°则∠A=;∠C=;∠D=;ABCD2、如图,ABCD中,BC=7,AB=5,它的周长为_________.ABCD130°130°50°241、一个平行四边形的一个外角是38°,这个四边形的每个内角的度数分别是多少?为什么?ABCDE38°当堂检测:2、如图,剪两张对边平行的纸条,随意交叉放在一起,转动其中一张,重合的部分构成了一个四边形.线段AD和BC的长度有什么关系?ADCB提高训练1.中,∠A比∠B大30∘,则∠A=__,∠D=__.ABCD3cmABDC5cm4cm提高训练2.求如图所示的平行四边形ABCD的面积.2212ABCABCDSScm四边形3cm2.ABCD中∠A比∠B大200,则∠C=————.2.ABCD中∠A比∠B大200,则∠C=————.2.ABCD中∠A比∠B大200,则∠C=————.第四章四边形性质探索小结ADBC定义表示方法性质两组对边分别平行的四边形叫做平行四边形。其不相邻的两个顶点连成的线段叫它的对角线。平行四边形ABCD,记为“□ABCD”,读作“平行四边形ABCD”,其中线段AC,BD称为对角线。平行四边形的对边平行且相等,对角相等,相邻两角互补。作业•P90:1,2