浙江省温州市龙湾中学高二数学-正弦定理课件VIP免费

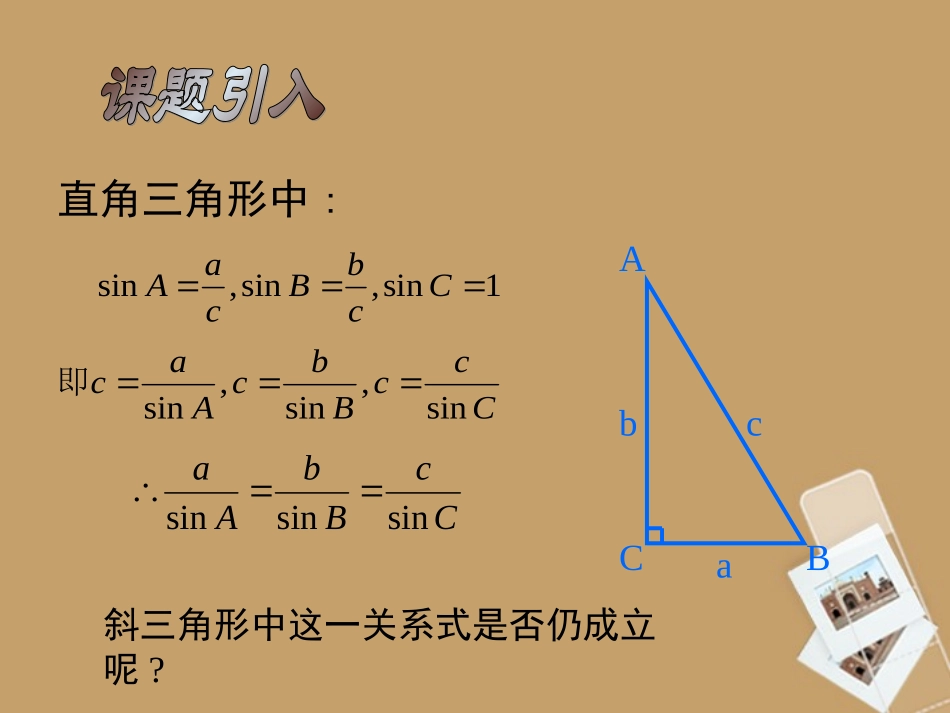
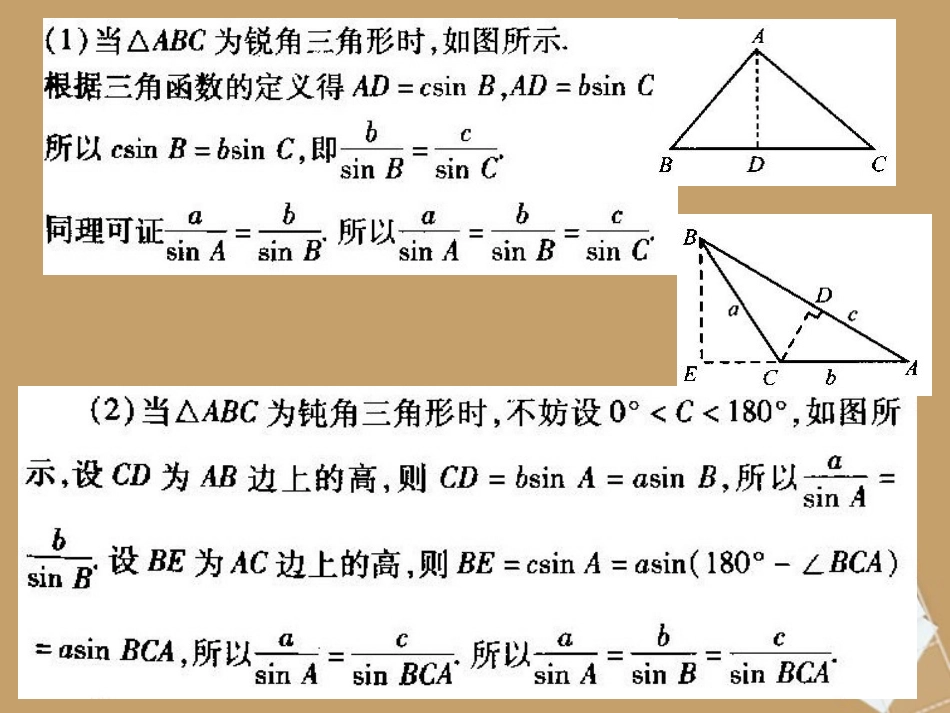
直角三角形中:1sin,sin,sinCcbBcaAABCabcCccBbcAacsin,sin,sin即CcBbAasinsinsin斜三角形中这一关系式是否仍成立呢?jABCjABCjCABj1CCRCcCc2sinsin1RAaRBb2sin2sin，同理：ABCC1abcO如图:为外接圆半径即得：RRCcBbAa2sinsinsin在一个三角形中,各边和它所对角的正弦的比相等,即为外接圆半径RRCcBbAa2sinsinsin变式:AaCcCcBbBbAasinsin;sinsin;sinsin1cbaCBA::sin:sin:sin2从理论上,正弦定理可解决两类问题:•两角和任意一边,求其他两边和一角•两边和其中一边对角,求另一边的对角,进而可求其他的边和角一般地，把三角形的三个角A,B,C和它的对边a,b,c叫做三角形的元素已知三角形的几个元素求其他元素的过程叫做解三角形例1:已知在中,,求和CA,1,60,3cBbaABC2.ABC0例在中，已知a=2,b=6,A=30，解三角形。•若A为锐角时:锐角一解一锐、一钝二解直角一解无解babaAbAbaAbasinsinsin若A为直角或钝角时:锐角一解无解baba练习：（1）在任一中，求证：ABC0)sin(sin)sin(sin)sin(sinBAcACbCBa证明：由于正弦定理：令CkcBkBAkasin,sin,sin左边＝代入左边得：)sinsinsinsinsinsinBCACABCBCABAksinsinsinsinsin(sin∴等式成立=右边02.在⊿ABC中，若acosA=bcosB,判断⊿ABC的形状？2.三角形面积计算公式通过本节学习通过本节学习,,我们一起研究了正我们一起研究了正弦定理的证明方法弦定理的证明方法,,同时了解了向量的工具性同时了解了向量的工具性作用作用,,并且明确了利用正弦定理所能解决的两并且明确了利用正弦定理所能解决的两类有关三角形问题类有关三角形问题::已知两角一边已知两角一边;;已知两边已知两边和其中一边的对角和其中一边的对角..