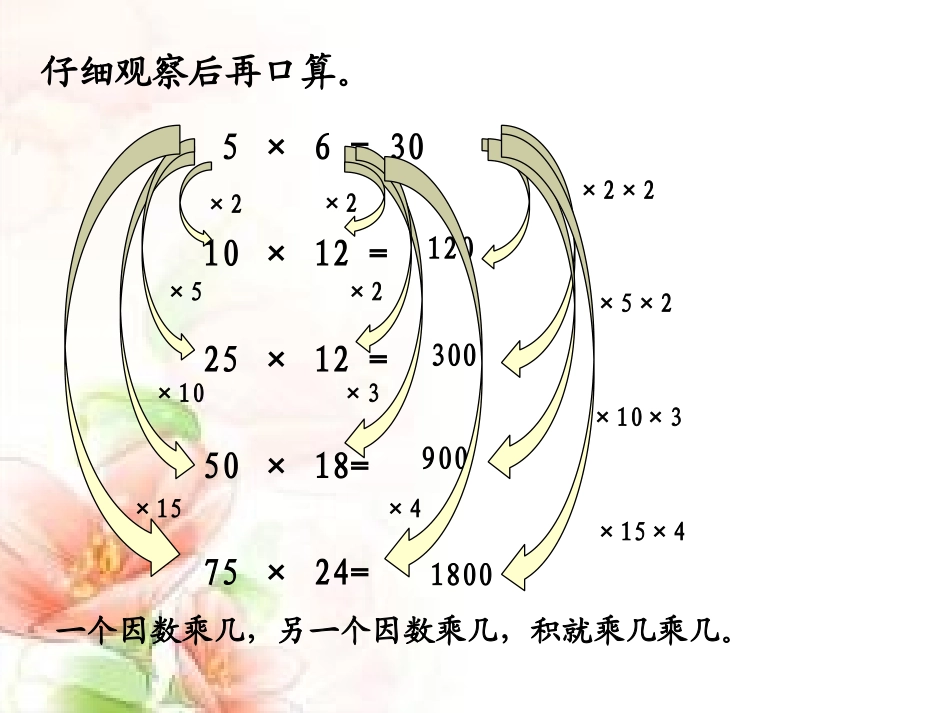
积的变化规律先计算出第一题,再快速地计算下面每题。4×13=16×2=4×130=16×6=4×1300=16×24=5232520520096384一个因数乘几,积也乘几。×10×10×10×10×3×3×4×44×13=5216×2=324×130=52016×6=964×1300=520016×24=384一个因数除以几,积也除以几。÷10÷10÷10÷10÷3÷3÷4÷45×6=3010×12=25×12=50×18=75×24=仔细观察后再口算。1203009001800一个因数乘几,另一个因数乘几,积就乘几乘几。×10×3×5×2×15×4×2×2×2×2×5×2×10×3×15×4根据12×5=60,直接写出下面各题的得数。24×25=24×15=120×15=96×25=60036018002400我们的猜想:(1)一个因数乘几,另一个因数乘几,积也乘几乘几。(2)一个因数除以几(0除外),另一个因数除以几(0除外),积也除以几除以几。(?)(3)一个因数乘几,另一个因数除以几(0除外),积也乘几除以几。(?)合作要求:1.4人小组小声讨论,有序合作,例举能体现“积的变化规律”的至少3道算式,并计算。2.合作完成后,先小组内说说你们的发现,然后组长指定汇报研究成果,其他同学认真倾听并思考。(1)一个因数乘几,另一个因数乘几,积也乘几乘几。(2)一个因数除以几(0除外),另一个因数除以几(0除外),积也除以几除以几。(3)一个因数乘几,另一个因数除以几(0除外),积也乘几除以几。我们验证的规律:1.两数相乘,一个因数乘10,另一个因数乘3,积就()。2.两数相乘,一个因数除以5,另一个因数除以2,积就()。3.两数相乘,一个因数乘8,另一个因数除以2,积就()。4.两数相乘,一个因数乘9,另一个因数除以9,积就()。5.两个因数的积是120。一个因数乘2,另一个因数乘3,积是()。6.两个因数的积是120。一个因数除以2,另一个因数除以3,积是()。7.两数相乘,一个因数乘2,要使积乘6,另一个因数应()。乘30除以10乘4不变72020乘3仔细观察,在里面填上合适的比较符号。24×75=1800(24×6)×(75×6)1800(24×3)×(75÷3)1800(24÷6)×(75÷3)1800(24×8)×(75÷5)1800>=<>我的收获: