平面与平面之间的位置关系高中数学人教版必修二VIP免费

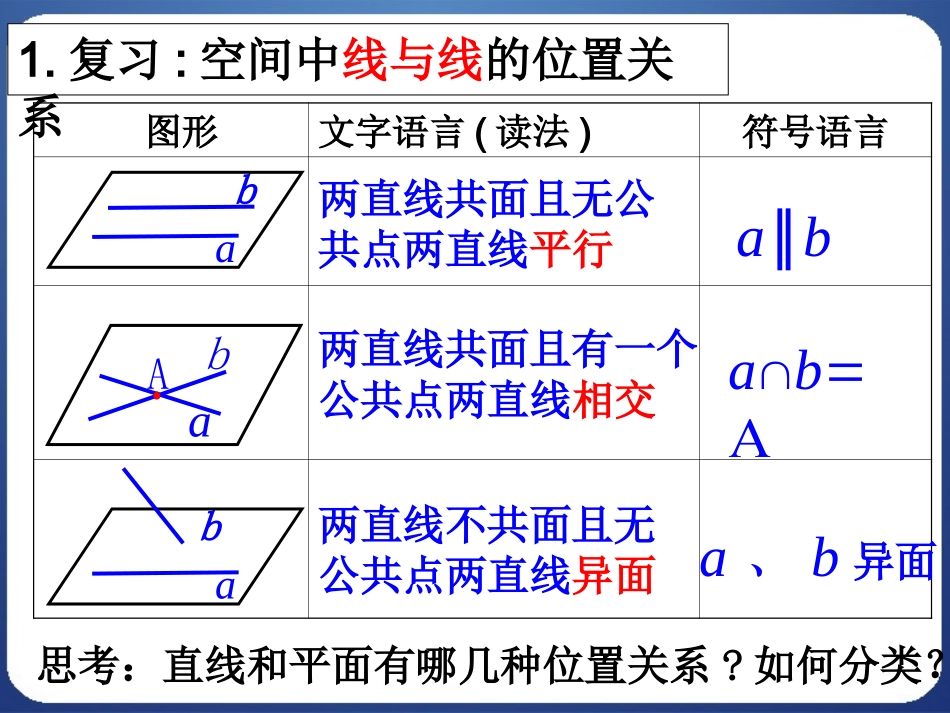
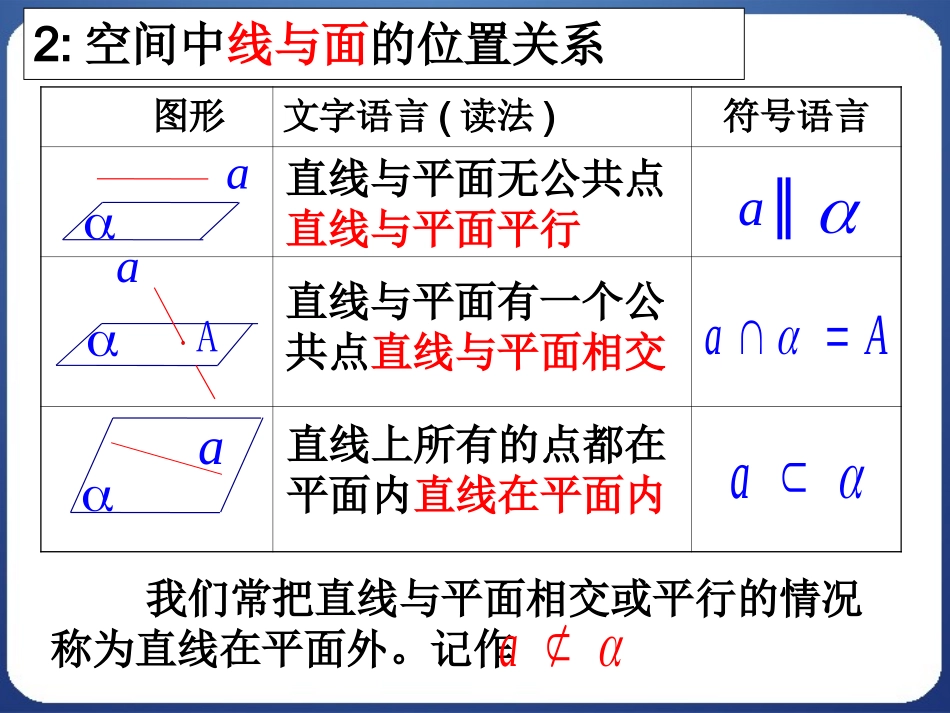
图形文字语言(读法)符号语言a∥b1.复习:空间中线与线的位置关系两直线不共面且无公共点两直线异面两直线共面且有一个公共点两直线相交两直线共面且无公共点两直线平行a、b异面abbaAbaba思考：直线和平面有哪几种位置关系?如何分类？图形文字语言(读法)符号语言aAaaAa∥2:空间中线与面的位置关系直线上所有的点都在平面内直线在平面内直线与平面有一个公共点直线与平面相交直线与平面无公共点直线与平面平行aa我们常把直线与平面相交或平行的情况称为直线在平面外。记作a研探新知:提出问题:空间中平面与平面的位置关系又是怎样的呢?观察思考:（1）拿出两本书，看作两个平面，上下、左右移动和翻转，它们之间的位置关系有几种？（2）如图，围成长方体AC1的六个面，两两之间的位置关系有几种？DCBAD'C'B'A'在问题（1）中，通过观察可以发现，两本书可以平行，也可以是相交，注意平面是无限延展的。在问题（2）中上下面，左右面，前后面是平行的，相邻的两个面是相交的，所以位置关系有平行与相交两种。DCBAD'C'B'A'两个平面之间的关系有且只有两种：（1）两个平面平行――没有公共点；（2）两个平面相交――有一条公共直线。想一想:分类的依据是什么样？两平面平行怎样画？相交又怎样画?画两个互相平行的平面时，要注意使表示平面的两个平行四边形的对应边平行图1图2×√两个平面的位置关系是:位置关系两平面平行两平面相交公共点符号表示图形表示没有公共点有一条公共直线∥aa探究21、一个平面把空间分为几部分？2、二个平面把空间分为几部分?3、三个平面把空间分为几部分?23或44或6或7或8了解一下：n个平面最多可将空间分为(n3+5n+6)/6个部分3.3个平面把空间分成几部分？探究2第三问图解：（2）（1）（3）（4）（5）46678例1.判断下列命题是否正确（1）若直线l上有无数个点不在平面内,则l//。（）（2）若直线l与平面平行，则l与平面内的任意一条直线都平行。（）（3）如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行.（）（4）若直线l与平面平行，则l与平面内的任意一条直线都没有公共点。（）X∨XX例题讲练例题讲练::例2、若直线a不平行平面，且则下列结论成立的是（）（A）内所有直线与a异面（B）内不存在与a平行的直线（C）内存在唯一的直线与a平行（D）内的直线与a都相交aB练习：1.如果三个平面两两相交，那么它们的交线有多少条？画出图形表示你的结论。答:有可能1条，也有可能3条交线。（1）（2）1．空间直线与直线的三种位置关系：(1)相交直线——同一平面内，有且只有一个公共点．(2)平行直线——同一平面内，没有公共点．(3)异面直线——不同在任何一个平面，没有公共点．2．空间直线与平面的三种位置关系(1)直线在平面内——有无数个公共点；(2)直线与平面相交——有且只有一个公共点；(3)直线与平面平行——没有公共点．直线与平面相交或平行的情况统称为直线在平面外．3．平面与平面的两种位置关系(1)两个平面平行——没有公共点；(2)两个平面相交——有一条公共直线．小结