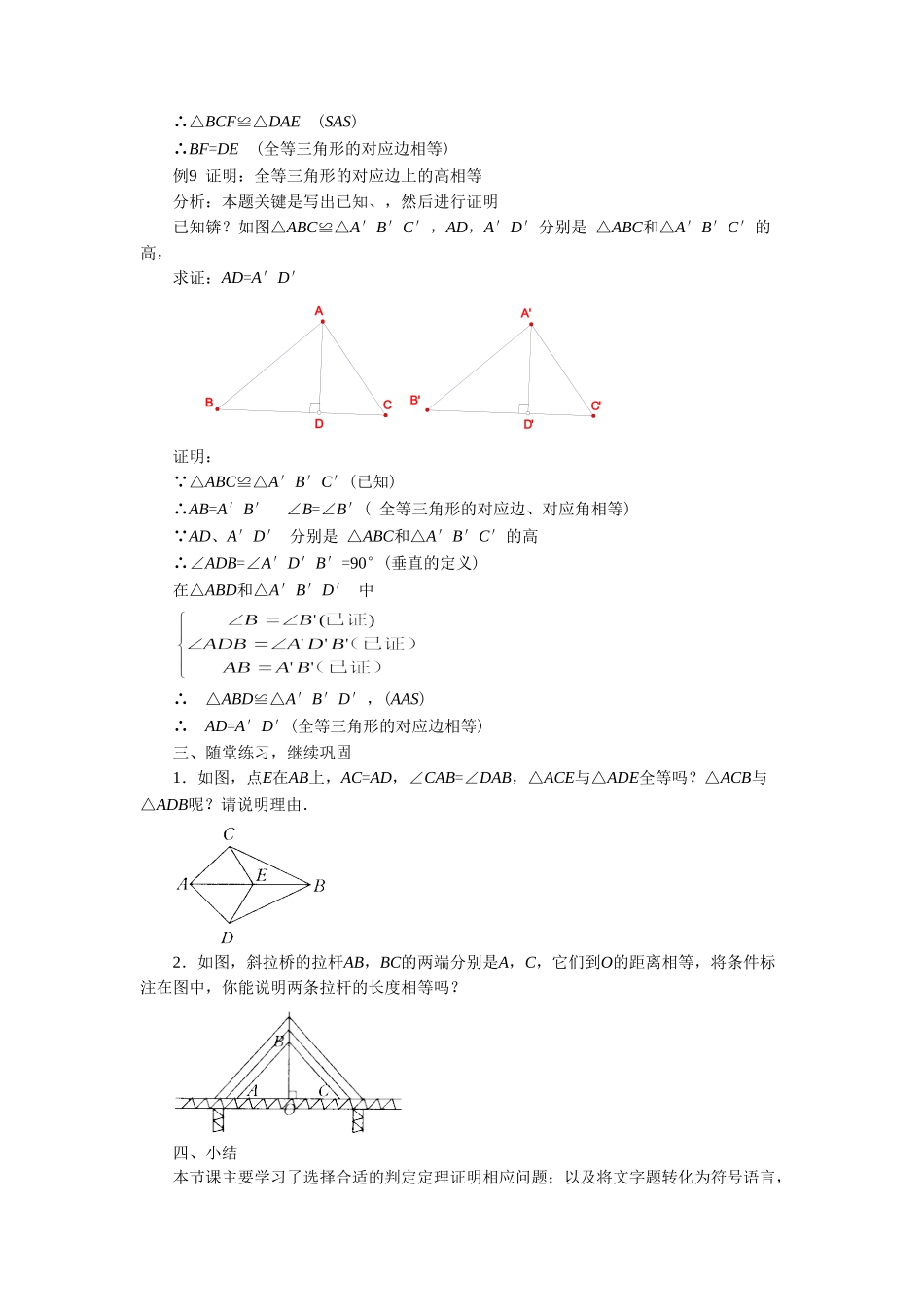
《三角形全等的判定》教案教学内容本节课主要内容是三角形全等的判定的综合运用.教学目标1.知识与技能理解三角形全等的判定,并会运用它们解决实际问题.2.过程与方法经历探索三角形全等的四种判定方法的过程,能进行合情推理.3.情感、态度与价值观培养良好的几何思维,体会几何学的应用价值.重、难点与关键1.重点:运用四个判定三角形全等的方法.2.难点:正确选择判定三角形全等的方法,充分应用“综合法”进行表达.3.关键:把握问题的因果关系,从中寻找思路.教学过程一、知识回顾前面我们已经学习过多种方法来证明三角形的全等,下面请同学们来说说有哪些方法.今天我们来用我们学过的几种方法来解决一些问题.二、例题分析例8.已知锛?如图AB=CD,BC=DA,E、F是AC上的两点,且AE=CF求证:BF=DE12DACBEF分析:本题需要两次证明三角形全等,首先证明△ABC≌△CDA(SSS)得出∠1=∠2,再由“边角边”定理证明△DAE≌△BCF最后证出BF=DE证明:在△ABC和△CDA中∵∴△ABC≌△CDA(SSS)∴∠1=∠2(全等三角形的对应角相等)在△BCF和△DAE中∵∴△BCF≌△DAE(SAS)∴BF=DE(全等三角形的对应边相等)例9证明:全等三角形的对应边上的高相等分析:本题关键是写出已知、,然后进行证明已知锛?如图△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的高,求证:AD=A′D′DABCD'A'B'C'证明:∵△ABC≌△A′B′C′(已知)∴AB=A′B′∠B=∠B′(全等三角形的对应边、对应角相等)∵AD、A′D′分别是△ABC和△A′B′C′的高∴∠ADB=∠A′D′B′=90°(垂直的定义)在△ABD和△A′B′D′中∴△ABD≌△A′B′D′,(AAS)∴AD=A′D′(全等三角形的对应边相等)三、随堂练习,继续巩固1.如图,点E在AB上,AC=AD,∠CAB=∠DAB,△ACE与△ADE全等吗?△ACB与△ADB呢?请说明理由.2.如图,斜拉桥的拉杆AB,BC的两端分别是A,C,它们到O的距离相等,将条件标注在图中,你能说明两条拉杆的长度相等吗?四、小结本节课主要学习了选择合适的判定定理证明相应问题;以及将文字题转化为符号语言,并与图形结合,写出已知、求证.