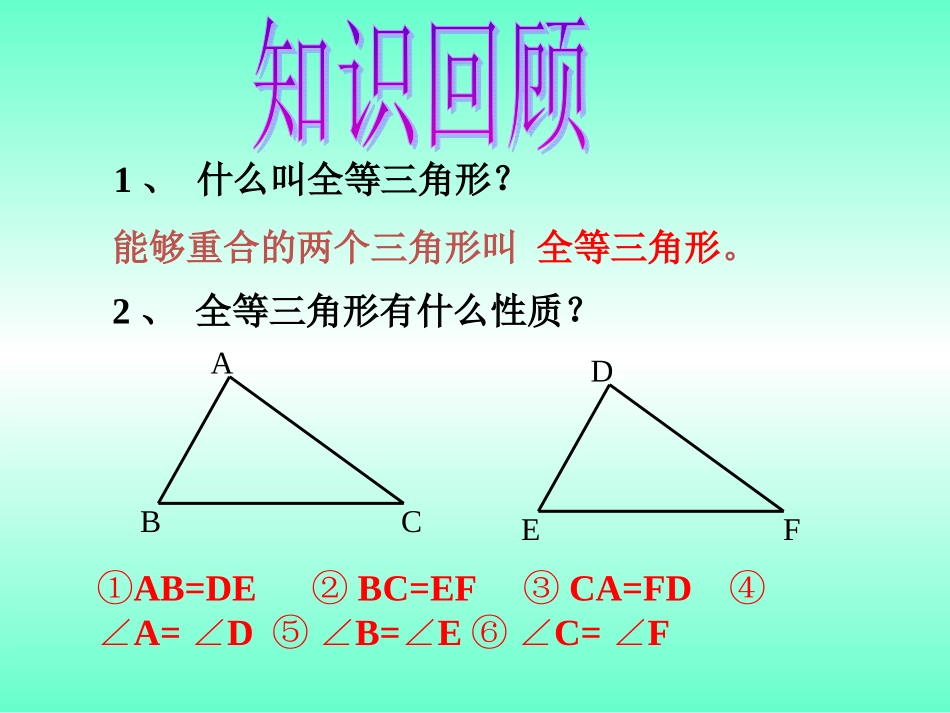
水冶镇一中牛艳丽§12.2三角形全等的判定第1课时(SSS)学习目标•1、掌握“边边边(SSS)”判定两个三角形全等的方法;•2、经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;•3、学会合作学习和探索精神。①AB=DEBC=EFCA=FD②③④A=DB=EC=F∠∠⑤∠∠⑥∠∠ABCDEF1、什么叫全等三角形?能够重合的两个三角形叫全等三角形。2、全等三角形有什么性质?1.只给一个条件(一组对应边相等或一组对应角相等)。①只给一条边:②只给一个角:60°60°60°2.给出两个条件:①一边一内角:②两内角:③两边:30°30°30°30°30°50°50°2cm2cm4cm4cm可以发现按这些条件画的三角形都不一定全等。画出一个三角形,使它的三边长分别为3cm、4cm、6cm,把你画的三角形与小组内画的进行比较,它们一定全等吗?画法:1.画线段AB=3㎝;2.分别以A、B为圆心,4㎝和6㎝长为半径画弧,两弧交于点C;3.连接线段AC、BC.结论:三边对应相等的两个三角形全等.可简写为“边边边”或“SSS”思考:你能用三角形的稳定性来说明“SSS”公理吗?有三边对应相等的两个三角形全等.可以简写成“边边边”或“SSS”ABCDEF用数学语言表述:在△ABC和△DEF中∴△ABCDEF≌△(SSS)AB=DEBC=EFCA=FDACBD分析:要证明两个三角形全等,需要哪些条件?证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABDACD≌△(SSS)例1.如图,ABC△是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,求证:△ABDACD≌△若要求证:∠B=C∠,你会吗?例2.作一个角等于已知角.已知:∠AOB1.如图,AB=AC,AE=AD,BD=CE,求证:△AEBADC≌△。证明:∵BD=CE∴BD-ED=CE-ED即BE=CD。在△AEB和△ADC中,AB=ACAE=ADBE=CD∴△AEBADC(sss)≌△CABDE(SSS)AABBCCDD2.2.如图,在四边形如图,在四边形ABCDABCD中中AB=CDAB=CD,,AD=BCAD=BC,则,则∠A=C∠请说明理由。解:解:在在△△ABDABD和和△△CDBCDB中中AB=CDAB=CD(已知)(已知)AD=BCAD=BC(已知)(已知)BD=DBBD=DB(公共边)(公共边)∴△△ABDABD≌△△CDBCDB∴∠A=∠C()全等三角形的对应角相等全等三角形的对应角相等如图1,AB=AD,CB=CD,求证:①△ABC≌△ADC;②∠B=∠D.点拨精讲:在证明过程中善于挖掘如“公共边”这个隐含条件,可以考虑添加辅助线。如图,AD=BC,AC=BD,求证(1)∠DAB=∠CBA(2)∠ACD=∠BDC点拨精讲:三角形全等的判定与性质的应用经常交替使用.如图所示,△ABC是一个风筝架,AB=AC,AD是连接A与BC中点D的支架,求证:AD⊥BCABCD通过这节课的学习,你有什么收获?本课小结1.必做题:练习册23页5-6题2.选做题:练习册23页学习拓展布置作业•不经历风雨,怎能见彩虹!•加油,相信你一定成功!