第七章演示稿VIP免费

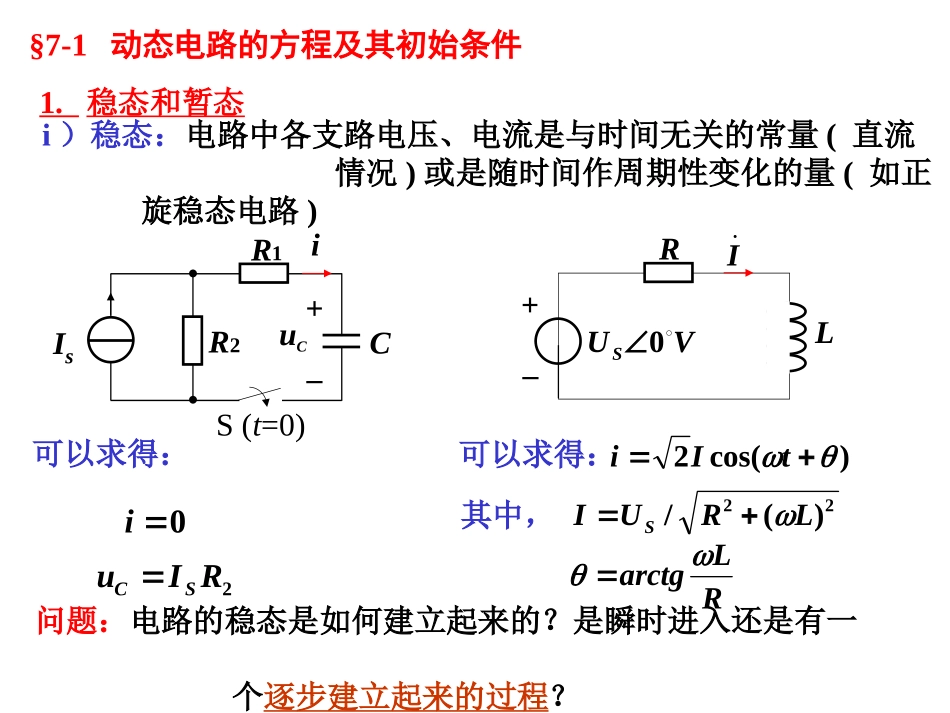
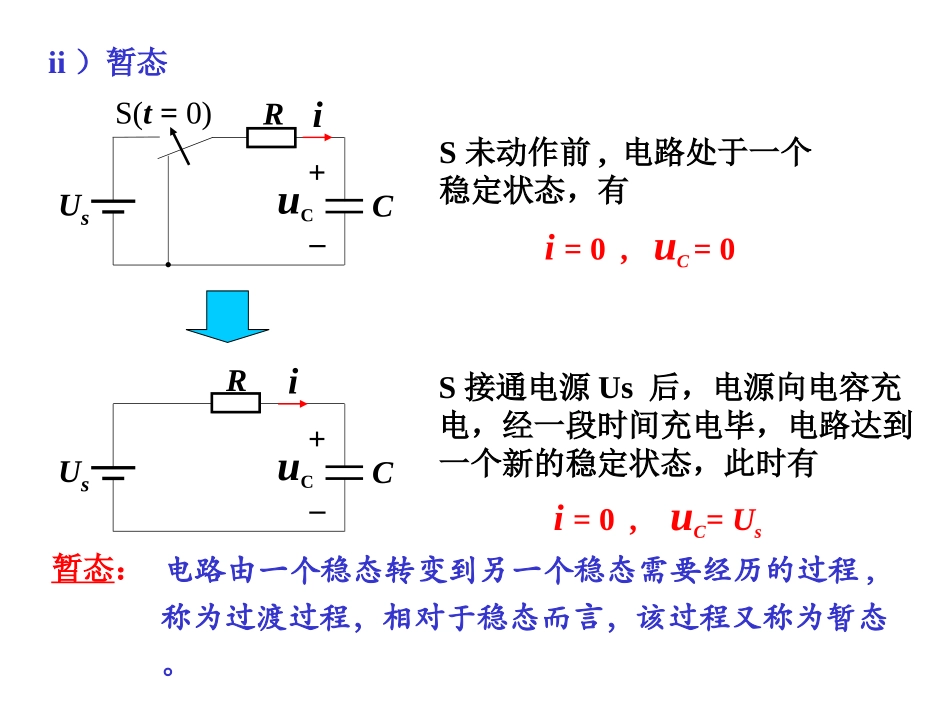
第七章一阶电路和二阶电路的时域分析2.零输入响应、零状态响应、全响应本章主要讨论一阶电路过渡过程的分析，重点掌握：3.阶跃响应和冲击响应1.一阶电路响应的求解：a)经典法b)简化的经典法——三要素方法§7-1动态电路的方程及其初始条件1.稳态和暂态i）稳态：电路中各支路电压、电流是与时间无关的常量(直流情况)或是随时间作周期性变化的量(如正旋稳态电路)问题：电路的稳态是如何建立起来的？是瞬时进入还是有一个逐步建立起来的过程？可以求得：0i2RIuSC+–uCIsR1CiR2S(t=0)可以求得：LIVUS0+–R)cos(2tIi22)(/LRUISRLarctg其中，ii）暂态暂态：电路由一个稳态转变到另一个稳态需要经历的过程,称为过渡过程，相对于稳态而言，该过程又称为暂态。S未动作前,电路处于一个稳定状态，有i=0,uC=0i=0,uC=UsS接通电源Us后，电源向电容充电，经一段时间充电毕，电路达到一个新的稳定状态，此时有+–uCUsRCiS(t=0)+–uCUsRCi2.过渡过程产生的原因外因：电源的接通或断开，电路参数的变化及联接方式的改变等，并统称为“换路”。内因：电路中有储能元件L、C。，那么：由WC＝Cuc2/2和WL＝LiL2/2若uc和iL突变，则WC和WL突变tdwdp这说明能量突变需要无穷大功率源，这实际上不可能。因此具有L、C的电路，一般uc和iL只能逐步变化。由于KCL和KVL的约束，导致电路中发生暂态过程。+–uCUsRCiS(t=0)iLSU+–R1S(t=0)R23.动态电路及其方程电路含动态元件L、C例：由KVL有：SUuRiCCduiCdt代入得：SUudtduRCCC当R、L、C都是线性元件时，电路的方程为线性常系数微分方程。用一阶微分方程描述的电路称为“一阶电路”。电路的阶：电路微分方程的阶。+–uCUsRCi描述动态电路的方程是微分方程动态电路i)关于t=0+与t=0–4.电路的初始条件初始条件为t=0+时u，i及其各阶导数的值换路在t=0时刻进行0–t=0的前一瞬间0+t=0后的初始瞬间0–0+0tf(t)求解微分方程需利用初始条件确定积分常数，而初始值一般是给定的或是根据换路定理分析换路前后的瞬时电路求得。当i()为有限值时00i()d0结论:换路瞬间，若电容电流保持为有限值,则电容电压(电荷)换路前后保持不变。q(0+)=q(0–)uC(0+)=uC(0–)ii)独立初始值q(0+)、uc(0+)、L(0+)和iL(0+)的计算对于电容元件C，有ditqtqtt)()()(00diCtututtcC)(1)()(00u=q/cd)()0()0(00iqqd)(1)0()0(00iCuucCa）q(0+)、uc(0+)的计算令t=0+及t0=0，有当u为有限值时结论:换路瞬间，若电感电压保持为有限值，则电感电流(磁链)换路前后保持不变。对于线性电感元件L，有duLtitittLL)(1)()(00dutttt)()()(00i=Ψ/LduLiiLL)(1)0()0(00du)()0()0(00b）L(0+)、iL(0+)的计算令t=0+及t0=0，有0L(0+)=L(0–)iL(0+)=iL(0–)；0归纳起来：换路定律uC(0+)=uC(0–)、q(0+)=q(0–)iL(0+)=iL(0–)、L(0+)=L(0–)根据换路前的稳态电路求出0–时刻的uC(0–)、q(0–)、iL(0–)及L(0–)值，然后由换路定理得到0+时刻的独立初始值uC(0+)、q(0+)、iL(0+)及L(0+)。独立初始值与换路后电路的结构、参数无关。iii）非独立初始值的计算0+等效电路换路后0+时刻的瞬时电路，其中电容用电压为uc(0+)的电压源替代，电感用电流为iL(0+)的电流源替代，独立源取的0+时刻的值，电阻不变——0+等效电路。先利用换路定律求独立的初始值，继而构造0+等效电路，然后在0+等效电路中用过去学过的一切方法求解非独立的初始值。由此可见：非独立的初始值决定于0+时刻的瞬时电路，是基尔霍夫定律约束的结果。非独立初始值计算0+等效电路8V+–10ViC+–10例1:电路如图,求iC(0+)。(1)由0–电路求uC(0–)(2)由换路定律uC(0+)=uC(0–)=8VA2.010810)0(Ci(3)作出0+等效电路并求iC(0+)iC(0–)=0iC(0+)uC(0–)=V84040101040+–uC10VCiCS(t=0)+–1040+–10ViC+–10uC(0–)VuL842)0(例2：电路如图，t=0时闭合开关S,求uL(0+))0(0)0(LLuu作出电路如图（b）解：iL(0+)=iL(0–)=4110=2A由...