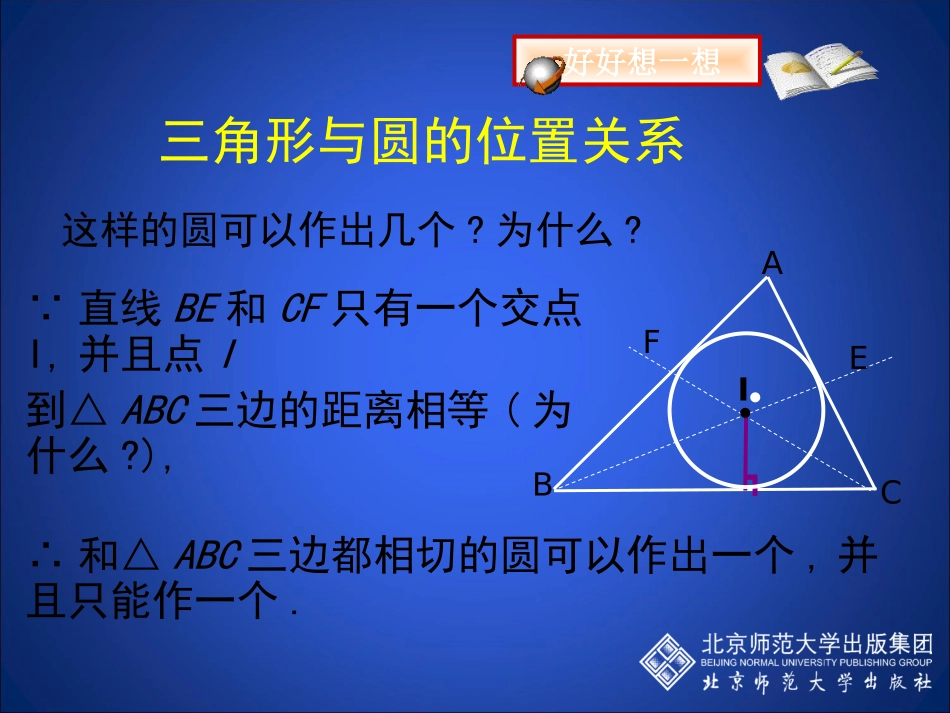
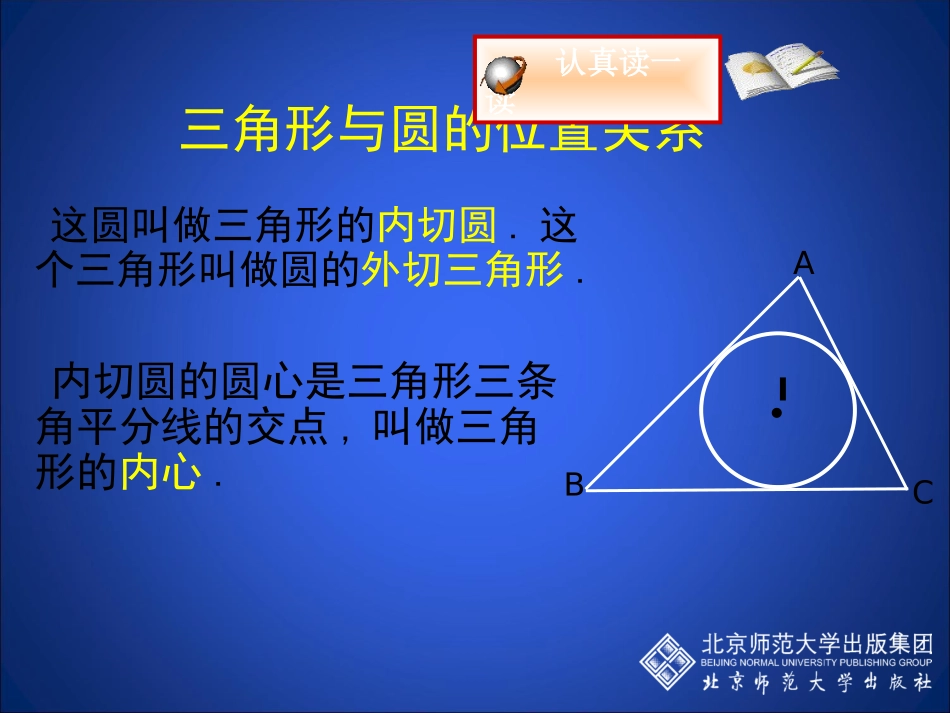
第三章圆3.7切线长定理广东佛山石门实验中学谭红良这样的圆可以作出几个?为什么? 直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),∴和△ABC三边都相切的圆可以作出一个,并且只能作一个.三角形与圆的位置关系ABCI●┓●EF好好想一想三角形与圆的位置关系这圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.认真读一读ABC●I三角形与圆的“切”关系1.以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?.练一练,你能行2.分别作出锐角三角形、直角三角形、钝角三角形的内切圆,并说明它们内心的位置情况.先确定圆心和半径,尺规作图要保留作图痕迹.ABCCAB┐ABC●●●一、创设情景,引入新课问题:有一天,同学们去王老师家做客,王老师正在洗锅,就问:谁能测出这个锅盖的半径,就可以得到一根雪糕,同学们都跃跃欲试,但老师家里只有一个曲尺,到底谁能得到这根雪糕呢?ABOPCDABOP二、合作学习,探究新知(一)、切线长定义1、切线长定义:在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的切线长.2、剖析定义:(1)找出中心词,把定义进行缩句。(线段的长叫做切线长)(2)定义中的“线段”具有什么特征?①在圆的切线上;②两个端点一个是切点,一个是圆外已知点。3、在图形中辨别:(1)已知:如图1,PC和⊙O相切于点A,点P到⊙O的切线长可以用哪一条线段的长来表示?图1PAO•从一块三角形材料中,能否剪下一个圆,使其与各边都相切?吸纳新知假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在这个三角形三个角的平分线上,半径为圆心到三边的距离.三角形与圆的位置关系ABCABC┓┗┗┓I●●●●┓┗┗┓┗┗┓┗┗I●┓●(2)已知:如图2,PA和PB分别与⊙O相切于点A、B,点P到⊙O的切线长可以用哪一条线段的长来表示?(线段PA或线段PB)(3)如图2,思考:点P到⊙O的切线长可以用三条或三条以上不同的线段的长来表示吗?这样的线段最多可以有几条?为什么?BOAP图2(4)既然点P到⊙O的切线长可以用两条不同的线段的长来表示,那么这两条线段之间一定存在着某种关系,是什么关系呢?BOAP图2(二)、切线长定理1、探索问题1:从⊙O外一点P引⊙O的两条切线,切点分别为A、B,那么线段PA和PB之间有何关系?探索步骤:(1)根据条件画出图形;(2)度量线段PA和PB的长度;(3)猜想:线段PA和PB之间的关系;(4)寻找证明猜想的途径;(5)在图3中还能得出哪些结论?并把它们归类。(6)上述各结论中,你想把哪个结论作为切线长的性质?请说明理由。2、由(6)得出定理:切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角. PA、PB分别是⊙O的切线,点A、B分别为切点,(PA、PB分别与⊙O相切于点A、B)∴PA=PB,∠APO=∠BPO.3、剖析定理:(1)指出定理的题设和结论;(2)用符号语言表示定理:ABPO图3(3)切线和切线长区别。切线是到圆心距离等于圆的半径的直线,而切线长是线段,指过圆外一点做圆的切线,该点到切点的距离。4、拓展:(1)图3是轴对称图形吗?连结图3中的两个切点AB交OP于点C,又能得出什么结论?并把它们分类。图4OPEDCBA答:图3是轴对称图形,连接AB,结论(1)△PAB是一个等腰三角形,并且存在等腰三角形的三线合一定理.(2)AB⊥OP,出现了圆的垂径定理.(2)已知圆O的两条切线互相平行,A、B两点为切点,如果连接两切点AB,则AB是圆O的直径吗?数学来源于生活,又应用于生活,请同学们再思考下,它们在我们的日常生活中各有什么应用?O图5EBFA(3)如图8中,作出三角形三条切线后与三角形各边都相切的圆叫做三角形的内切圆,图8中存在切线长定理吗?.图8OOO存在(三)、圆的外切四边形的性质请同学们先在草稿本中作出有关已知圆O的四条切线,再互相交流与讨论你的发现与结论并加以验证.图9ODCBA结论:圆的外切四边形的两组对边的和相等.例题1:已知如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O是△ABC的内切圆,切点分别为D,E,F,求⊙O的半径。例题1图AFBDEOC•变式1:如...