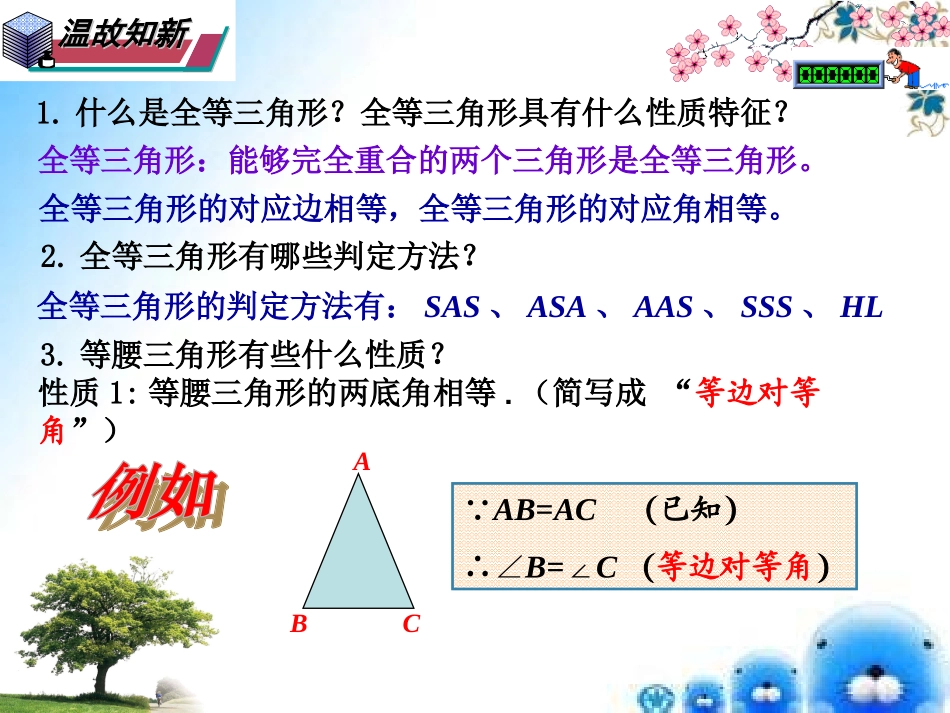
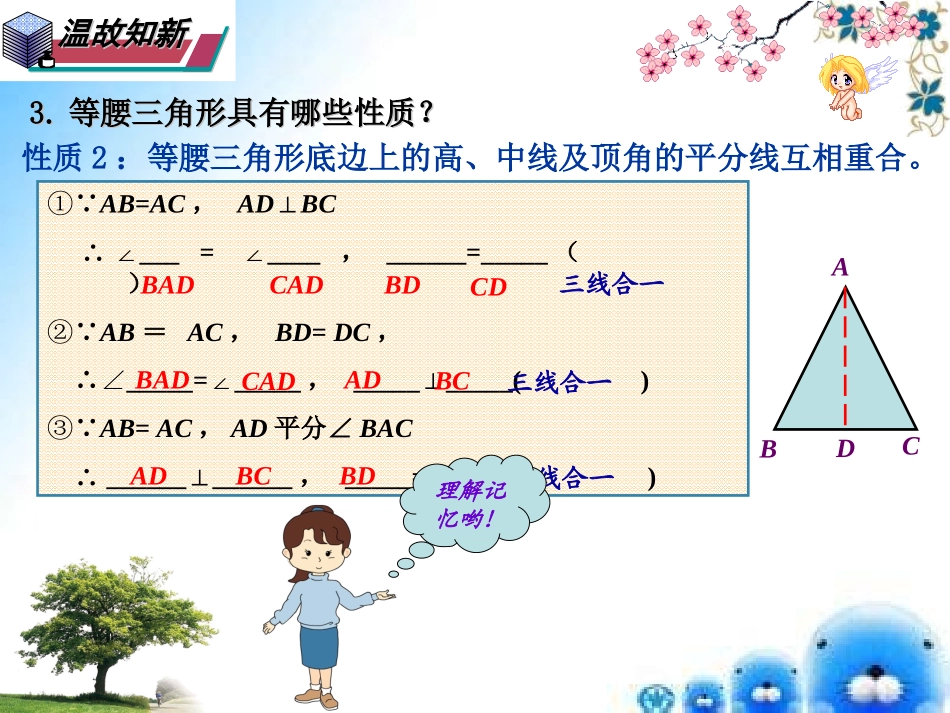
温故知新温故知新1.什么是全等三角形?全等三角形具有什么性质特征?全等三角形:能够完全重合的两个三角形是全等三角形。全等三角形的对应边相等,全等三角形的对应角相等。2.全等三角形有哪些判定方法?全等三角形的判定方法有:SAS、ASA、AAS、SSS、HL3.等腰三角形有些什么性质?性质1:等腰三角形的两底角相等.(简写成“等边对等角”)ABC∵AB=AC(已知)∴∠B=∠C(等边对等角)温故知新温故知新3.3.等腰三角形具有哪些性质?等腰三角形具有哪些性质?CBAD性质2:等腰三角形底边上的高、中线及顶角的平分线互相重合。简称“三线合一”①∵AB=AC,AD⊥BC∴∠___=____∠,______=_____()②∵AB=AC,BD=DC,∴∠_____=_____∠,__________()⊥③∵AB=AC,AD平分∠BAC∴____________⊥,_____=____()BADCADBDCD三线合一BADCADADBC三线合一三线合一ADBCBDCD理解记忆哟!华师版第13章全等三角形八年级(上)探究发现探究发现例1(教材81页练习3改编)如图1,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E.(1)请问BD=CE吗?如果相等,请证明你的结论?(2)OB、OC有什么样的数量关系?请加以证明。分析:△BCE≌△CBD角:角:边:∠BEC=∠CDB要得到BD=CE∠EBC=∠DCBBC=CB请你书写论证过程!在△BEC和△CDB中∴△BEC△△CDB(AAS)∴CE=BD∵AB=AC又∵BD⊥AC,CE⊥AB解:BD=CE,理由如下:∴∠ABC=∠ACB∴∠BEC=∠CDB=90°∠BEC=∠CDB∠ABC=∠ACBBC=CB还有另外的解法吗!∴∠DBC=∠ECB∴OB=OC图1EODACB变换1:如果将“BD⊥AC,CE⊥AB,垂足分别为D、E”改为“BD、CE是△ABC的中线”,请问上述结论仍然成立吗?探究发现探究发现例2(1)请问BD=CE吗?如果相等,请证明你的结论?(2)OB、OC有什么样的数量关系?请加以证明。分析:△BCE≌△CBD边:角:边:BE=CD要得到BD=CE∠EBC=∠DCBBC=CB请你书写论证过程!图2EODACB如图2,在△ABC中,AB=AC,BD、CE是△ABC的中线。变换2:如果将“BD、CE是△ABC的中线”改为“BD、CE是△ABC的角平分线”,请问上述结论仍然成立吗?探究发现探究发现例3(1)请问BD=CE吗?如果相等,请证明你的结论?(2)OB、OC有什么样的数量关系?请加以证明。分析:△BCE≌△CBD角:边:角:要得到BD=CE∠EBC=∠DCBBC=CB有何感悟!图3EODACB如图3,在△ABC中,AB=AC,BD、CE是△ABC的角平分线.∠ECB=∠DBC发现之旅发现之旅1.证明线段和角相等,常用的方法是证明包含着线段和角的两个三角形全等。2.涉及创新思维类型的题目时,注意(1)后面变换的题型的作法同前面类似;(2)如果一题有多问,一般后面要利用前面的结论。记住解题技巧哟!拓展延伸拓展延伸图4EFDACB例4如图4,在△ABC中,AB=AC,D为BC的中点,过点D作DF⊥AC,DE⊥AB,垂足分别为E、F.变换3:若将例1的“在△ABC中,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E.”改为“D为BC的中点,过点D作DF⊥AC,DE⊥AB,垂足分别为E、F”,请问DE、DF有什么数量关系?(1)请问DE、DF有什么数量关系,并加以证明?(2)过点C作CG⊥AB于G,请问DE、DF、CG之间有什么关系?请论证。图1EODACBG12H拓展延伸拓展延伸图4EFDACB例5如图5,在△ABC中,AB=AC,D为BC上任意点,过点D作DF⊥AC,DE⊥AB,过点C作CG⊥AB于G,垂足分别为E、F、G.请问DE、DF、CG之间有什么关系?请论证。变换4:如果将例4的“D为BC的中点”改为“D为BC上的任意一点”其余条件不变,请问DE、DF、CG的数量关系是否依然成立?图5EFDACBG我的收获是……这节课我学到了什么?我还有……的疑惑小结小结归纳总结归纳总结图5EFDACBG图1EODACB图2EODACB图3EODACB图4EFDACBG经典数学…如图,在△ABC中,AB=AC,D为BC上延长线上任意点,过点D作DF⊥AC,DE⊥AB,过点C作CG⊥AB于G,垂足分别为E、F、G.请问DE、DF、CG之间有什么关系?请论证。EFDACBG数学活动室,拓展加深仔细想一想哟!复习题复习题BB组组P105P105第11-15题一个人一天也不能没有理想,凭侥幸、怕吃苦、没有真才实学,再好的理想也不能实现不了。