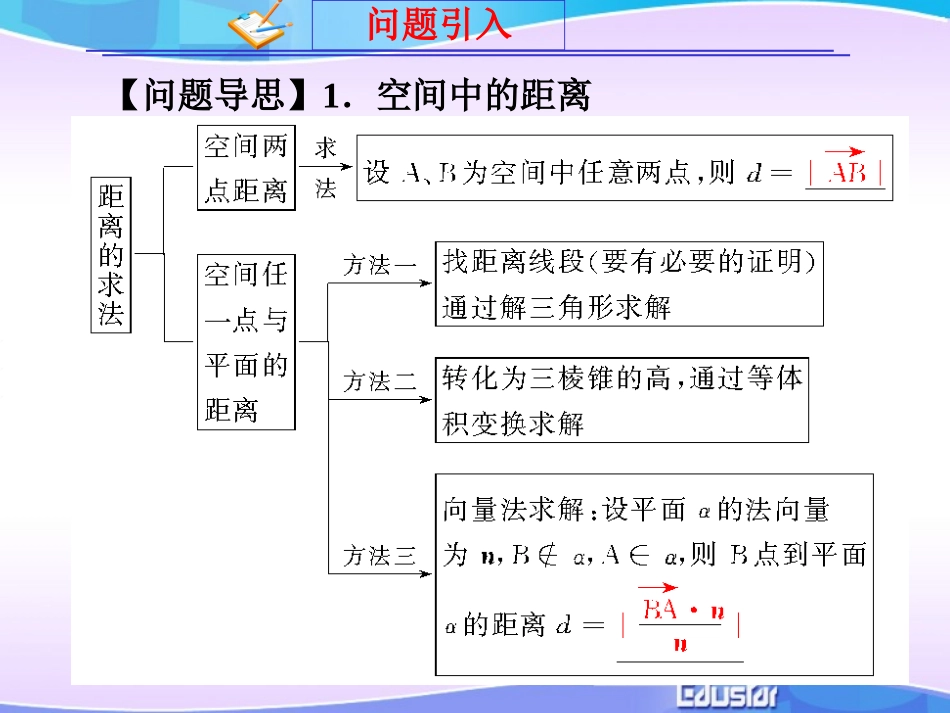
选修2-1第4课时空间向量与空间距离课标解读【课标要求】【学习重点】两点间的距离,点到平面的距离【学习难点】两异面直线间的距离,线面距、面面距向点面距的转化.1.理解点到平面的距离的概念.2.能灵活运用向量方法求各种空间距离.3.体会向量法在求空间距离中的作用.问题引入【问题导思】1.空间中的距离问题导思想一想:在求两条异面直线间的距离,直线到平面的距离,两个平面间的距离时能转化为点到平面的距离求解吗?因为直线与平面平行,两个平面平行时,直线上的点或其中一个平面上的点到另一个平面的距离均相等,而两条异面直线可以构造线面平行,所以在求以上距离时均可转化为点到平面的距离.问题导思点到平面距离的求法如图,BO⊥平面α,垂足为O,则点B到平面α的距离就是线段BO的长度.若AB是平面α的任一条斜线段,则在Rt△BOA中,|BO→|=|BA→|·cos∠ABO=|BA→|·|BO→|·cos∠ABO|BO→|.如果令平面α的法向量为n,考虑到法向量的方向,可以得到B点到平面α的距离为|BO→|=|AB→·n||n|.问题导思由于n|n|=n0可以视为平面的单位法向量,所以点到平面的距离实质就是平面的单位法向量与从该点出发的斜线段向量的数量积的绝对值,即d=|AB→·n0|.因此用向量法求一个点到平面的距离,可以分以下几步完成:(1)求出该平面的一个法向量;(2)找出从该点出发的平面的任一条斜线段对应的向量;(3)求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即可求出点到平面的距离.题型探究题型一、求两点间的距离如图,正方形ABCD和ABEF的边长都是1,且它们所在平面互相垂直,点M在AC上,点N在BF上.若CM=BN=22,求MN的长.【例1】变式训练如图所示,在120°的二面角αABβ中,AC⊂α,BD⊂β且AC⊥AB,BD⊥AB,垂足分别为A、B,已知AC=AB=BD=6,试求线段CD的长.规律方法求两点间的距离的向量法主要是坐标法(易建系的)和基向量法(各基向量的模和夹角已知或可求),利用向量模的定义求解.题型探究题型二、求点到直线的距离【例2】正方体ABCD-A1B1C1D1的棱长为1,利用向量法求点C1到A1C的距离.规律方法利用向量求点线距时,不用找到点在直线上的垂足,直接按向量法的求解步骤来求就行,同时线上的点可以任意取,但一般选择特殊点,同时直线的方向向量也可以任意取.变式训练如图,P为矩形ABCD所在平面外一点,PA⊥平面ABCD,若已知AB=3,AD=4,PA=1,求点P到BD的距离.题型探究题型三、求点到平面的距离规律方法【题后反思】用向量法求点面距的方法与步骤:(1)建坐标系:结合图形的特点建立恰当的空间直角坐标系;(2)求向量:在坐标系中求出点到平面内任一点对应的向量AB→;(3)求法向量:设出平面的法向量,利用向量垂直的条件转化为求解方程组,求出法向量n;(4)得答案:代入公式d=|AB→·n||n|求得答案.变式训练正方体ABCD-A1B1C1D1的棱长为2,E、F、G分别是C1C,D1A1,AB的中点,求点A到平面EFG的距离.课后作业《课本》P.112:A组:5、9B组:1、2空间距离在高考中考查较多的是两点距和点面距.两点距主要利用向量的模即两点间的距离公式求解.点面距利用平面的法向量代入公式求解.有了向量,距离的求法也都公式化了.