341基本不等式证明（1）VIP免费

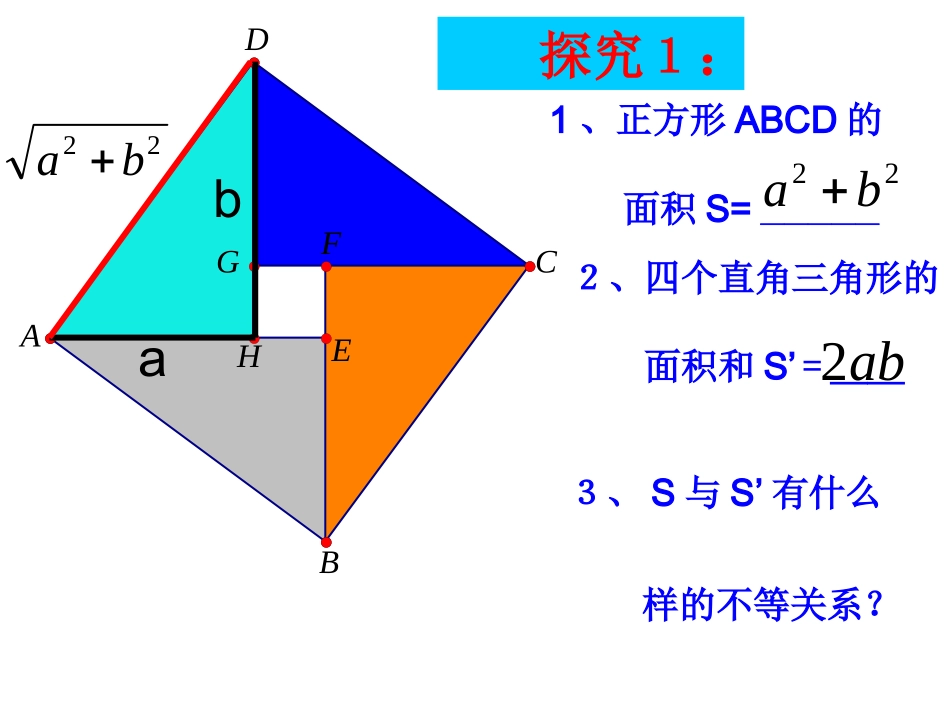
3.4.13.4.1基本不等式的证明基本不等式的证明这是2002年在北京召开的第24届国际数学家大会会标．会标根据中国古代数学家赵爽的弦图设计的，颜色的明暗使它看上去象一个风车，代表中国人民热情好客。ADCBHFGEab22ba22ba1、正方形ABCD的面积S=＿＿＿＿＿２、四个直角三角形的面积和S’=＿＿ab2３、S与S’有什么样的不等关系？探究１：结论１重要不等式:变形公式：文字叙述为:两数的平方和不小于积的2倍。若a,bR∈，那么a2+b2≥2ab（当且仅当a=b时，取“=”号）222abab那么a2+b2≥2ab那么a+b≥2（当且仅当a=b时，取“=”号）若aR,b∈∈Rb若a>0b>0a如果a>0,b>0,我们用去替换a、b,能得到什么结论?探究２：,ab（当且仅当a=b时，取“=”号）结论２基本不等式2abab(>0,b>0)a探究3：ABCDE1、如图,AB是圆的直径，C是AB上与A、B不重合的一点，AC=a,CB=b,过点C作垂直于AB的弦DE，连AD,BD,则CD=＿＿,半径=＿＿＿＿２、你能用这个图形得出基本不等式几何解释吗?abab2ba半弦不大于半径(a>0,b>0)2abab•我们把叫做a,b的算术平均数，把叫做a,b的几何平均数；•文字叙述为：两个正数的算术平均数不小于不小于它们的几何平均数，因此也叫均值不等式；•从形的角度来看，基本不等式具有特定的几何意义；从数的角度来看，基本不等式揭示了“和”与“积”这两种结构间的不等关系；•正用、逆用，注意成立的条件⑴a、b是两个正数；⑵当且仅当a=b时“＝”号成立。2abab剖析公式(a>0,b>0)2abab个数的算术平均数叫做这nnaaan21个数的几何平均数叫做这naaann21naaan21≥nnaaa21niRaNni1,,*推广例1.已知,,abcR求证：222abcabbcca证：∵222abab222bcbc222caca以上三式相加：2222()222abcabbcca222abcabbcca∴当且仅当a=b=c时等号成立练习.8))()((,,,.1abcaccbbacba求证都是正数已知证明:,02abba,02acac,02bccb.88))()((abccabcabaccbba当且仅当a=b=c时等号成立练习abbaabbaRba2.,,求证且证明:abbaba2,abababbaab222例1、若x>0，求的最小值xxy1变式：若x>3,求的最小值31xxy构造条件利用不等式求最值问题),(2Rbaabba1xx当x=1时，有最小值2。110,22xxxxx解：1xx当且仅当＝时，即x=1时取“＝”一正,二定,三相等③必须有自变量的值能使函数取到=号.①函数式中相关项必须为正;②所求函数式中,含变数的各项和或积必须为定值;利用均值不等式求函数最值应注意:2212()313fxxx例：求的最小值例3（1）.用篱笆围一个面积为100m2矩形菜园，问这个矩形的长、宽各为多少时，所用篱笆最短，最短的篱笆是多少？解:(1)设矩形菜园的长为xm,宽为ym,则xy=100,篱笆的长为2(x+y)m.解:(1)设矩形菜园的长为xm,宽为ym,则xy=100,篱笆的长为2(x+y)m.40.xy2()等号当且仅当x=y时成立,此时x=y=10.等号当且仅当x=y时成立,此时x=y=10.因此,这个矩形的长﹑宽都为10m时,所用篱笆最短,最短篱笆是40m.因此,这个矩形的长﹑宽都为10m时,所用篱笆最短,最短篱笆是40m.由由,2xyxy2100xy可得,Ex1:已知直角三角形的面积等于50，两条直角边各为多少时，两条直角边的和最小，最小值是多少？结论1：两个正数积为定值，则和有最小值20例3（2）.用一段长为36m的篱笆围成一个矩形菜园，问这个矩形菜园的长和宽各为多少时，菜园的面积最大，最大面积是多少？81,xy可得等号当且仅当x=y,即x=y=9时.等号成立.等号当且仅当x=y,即x=y=9时.等号成立.解:(2)设矩形菜园的长为xm,宽为ym,则2(x+y)=36,x+y=18,矩形菜园的面积为xy解:(2)设矩形菜园的长为xm,宽为ym,则2(x+y)=36,x+y=18,矩形菜园的面积为xy2m因此,这个矩形的长﹑宽都为9m时,菜园面积最大,最大面积是81因此,这个矩形的长﹑宽都为9m时,菜园面积最大,最大面积是812m由由189,22xyxyEx:用20cm长的铁丝折成一个面积最大的矩形,应当怎样折?结论2：两个正数和为定值，则积有最大值课堂小结1、本节课主要学习了基本不等式的证明与初步应用。2、注意公式的正向、逆向使用的条件以及“=”成立的条件。（１）若a,bR∈，那么a2+b2≥2ab（当且仅当a=b时，取“=”号）（2）（当且仅当a=b时，取“=”号）0,0,2ababab若那么3、会用基本不等式解决简单的最大(小)值问题。