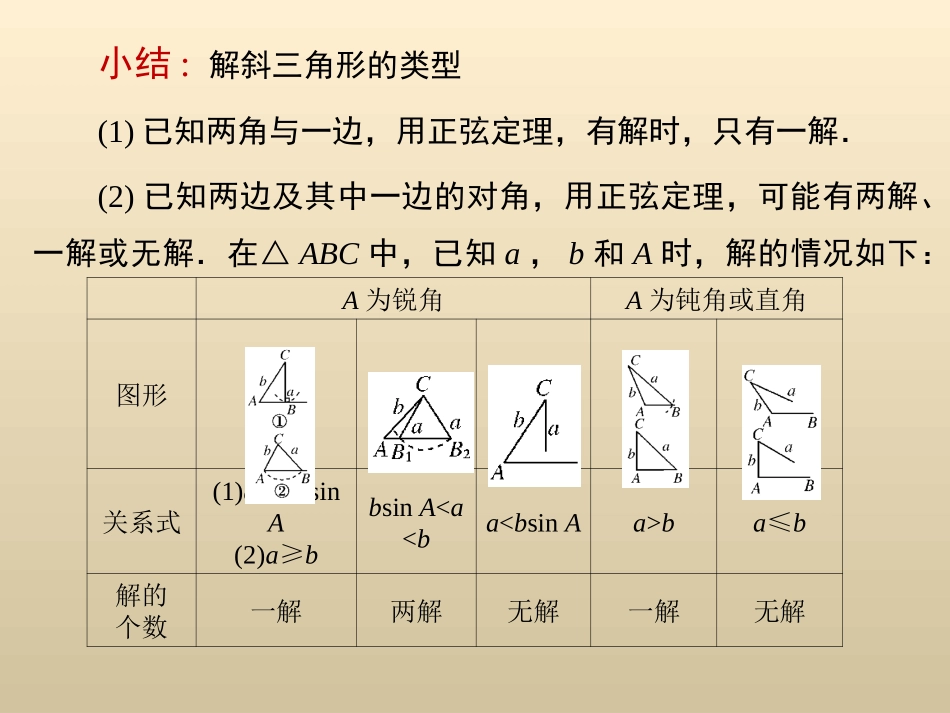
正余弦定理习题课正余弦定理习题课0,102,45.20320,,53.1:,ABCABABCC在中已知在边的长分别为的情况下求相应的例小结:解斜三角形的类型(1)已知两角与一边,用正弦定理,有解时,只有一解.(2)已知两边及其中一边的对角,用正弦定理,可能有两解、一解或无解.在△ABC中,已知a,b和A时,解的情况如下:A为锐角A为钝角或直角图形关系式(1)a=bsinA(2)a≥bbsinA
ba≤b解的个数一解两解无解一解无解0,,2,45.,:.ABCaxbBx在中已知若这个三角形有两解求习的取值范围练三角形形状的判断:,lglglgsinlg2,:,ABCacBB在中已知且为锐角试判断此三角形例2的形状.思路一:正弦定理,边角代换.思路一:余弦定理.:coscos,ABCaAbB练习在中,如果有性质试判断这个三角形的形状。•[题后感悟](1)确定三角形的形状主要有两条途径:•①化边为角;②化角为边.•(2)确定三角形形状的思想方法:先将条件中的边角关系由正弦定理统一为角角或边边关系,再由三角变形或代数变形分解因式,判定形状.在变形过程中要注意等式两端的公因式不要约掉,应移项提取公因式,否则会有漏掉一种解的可能.练习2:在△ABC中,(b+c+a)·(b+c-a)=3bc,且sinA=2sinB·cosC。试确定△ABC的形状。正余弦定理的综合应用:23,cos()cos,:.2ABCACBbacB例3在中已知求.,5,3,sin2sin.(1);(2)sin(24:ABCBCACCAABA在中求例4的值求)的值.链接高考:2010浙江.理科