不等式的简单变形（修改版）VIP免费

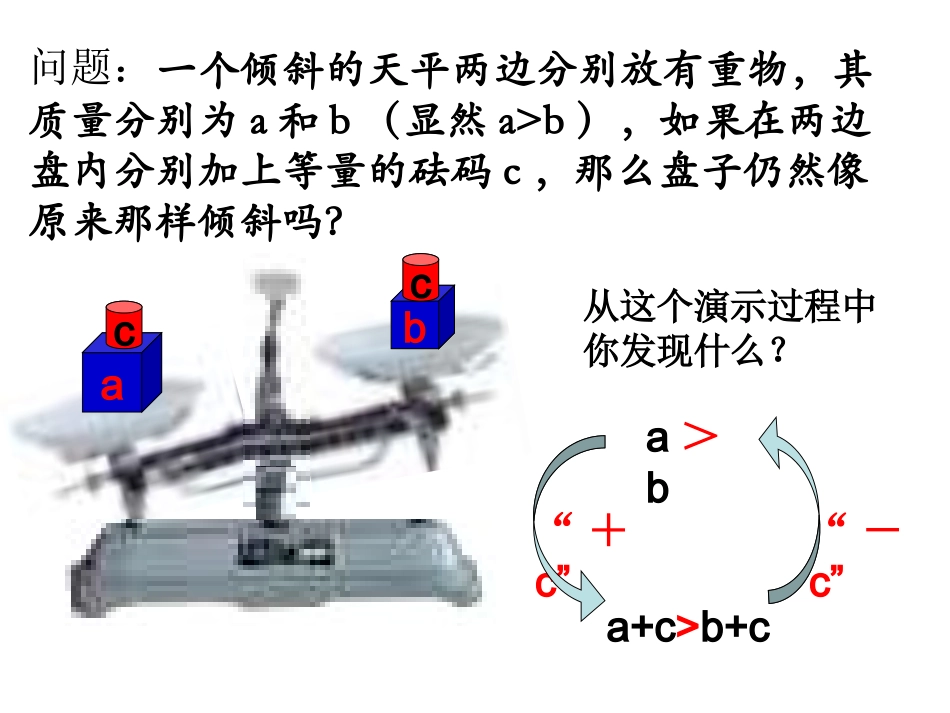
1、说明下列等式变形的理由：移项变号等式性质1：等式两边同时加(减)同一个数或式子，等式仍然成立。32x23x复习2、说明下列等式变形的理由：321x23x系数化为1等式性质2：等式两边同时乘以(除以)同一个不为零的数，等式仍然成立。321x23x复习问题：一个倾斜的天平两边分别放有重物，其质量分别为a和b（显然a>b），如果在两边盘内分别加上等量的砝码c，那么盘子仍然像原来那样倾斜吗？abcca＞ba+c>b+c“＋c”从这个演示过程中你发现什么？“－c”回忆1“．用<”“或>”号填空：（1）7______4；7＋3____4＋3；7－3_____4－37＋4____4+4；7－4_____4－4（2）若a＞b；a＋c____b＋ca－c____b－c思考：不等式两边同时加上或减去一个相同的数c不等式还成立吗？＞＞＞＞＞abcca＞ba+c>b+c“＋c”“－c”从这个演示过程中你发现什么？不等式两边加（或减去）同一个数（或式），不等号的方向不变.不等式的性质1如果a>b,那么a±c>b±c(1)67xax例1、利用不等式性质把下列不等式变形为“”或“”的最简形式：ax67x7677x76x76x移项13x移项不等式两边加（或减去）同一个数（或式），不等号的方向不变等式两边同时加(减)同一个数或式子，等式仍然成立巩固ax1、利用不等式性质把下列不等式变形为:“”或“”的形式：ax(1)x23(2)2213xx思考：不等式的两边同时乘以同一个数，不等号的方向是否也不变呢？1、将不等式7>4两边都乘以同一个数，比较所得的数的大小，用“<”或“>”填空：7×3_______4×3，7×2_______4×2，7×1_______4×1，7×0_______4×0，7×（－1）_______4×（－1），7×（－2）_______4×（－2），7×（－3）_______4×（－3），………………………………………………从中你能发现什么？＞＞＞=<<<1、将不等式7>4两边都乘以同一个数，比较所得的数的大小，用“<”或“>”填空：7×3_______4×3，7×2_______4×2，7×1_______4×1，7×0_______4×0，从中你能发现什么？＞＞＞=概括（不等式的性质2）如果a>b，并且c>0，那么ac>bc。不等式的性质2：不等式两边都乘以（或除以）同一个正数，不等号的方向不变(1)62xax例2、利用不等式性质把下列不等式变形为“”或“”的最简形式：ax62x2622x2622x系数化为13x系数化为1不等式两边都乘以（或除以）同一个正数，不等号的方向不变等式两边同时乘以(除以)同一个不为零的数，等式仍然成立巩固ax(1)26x2、利用不等式性质把下列不等式变形为:“”或“”的形式：ax(2)432x1、将不等式7>4两边都乘以同一个数，比较所得的数的大小，用“<”或“>”填空：7×（－1）_______4×（－1），7×（－2）_______4×（－2），7×（－3）_______4×（－3），………………………………………………从中你能发现什么？<<<概括（不等式的性质3）如果a>b，并且c<0，那么acb，用“<”或“>”填空并说明理由：(1)a-5______b-5;(2)a+4_____b+4;>>><;31_____31ba(3)6a______6b;(4)(5)2a-3____2b-3;(6)-3.5a+1____-3.5b+1><看谁做得快例1、解不等式：（1）x－7<8（2）3x<2x-3巩固练习解:（1）不等式的两边都加上_____，不等式的_________，所以x－7_____<8_____，得x_____+7+77<15（2）不等式的两边都减去_____（即加上_____），不等号的_________，所以3x_____<2x－3_____得x_____2x－2x－2x－2x<－3方向不变方向不变巩固练习解:（1）不等式的两边都乘以_____，不等式的_________，所以得x>-6262232112xx)(）、（、解不等式：例_____________321x22（2）不等式的两边都除以_____（乘以_____，不等式的_________，所以得x_________－2_______6______2x)21(－1/2方向改变方向不变)21(>－3解:（1）不等式的两边都乘...