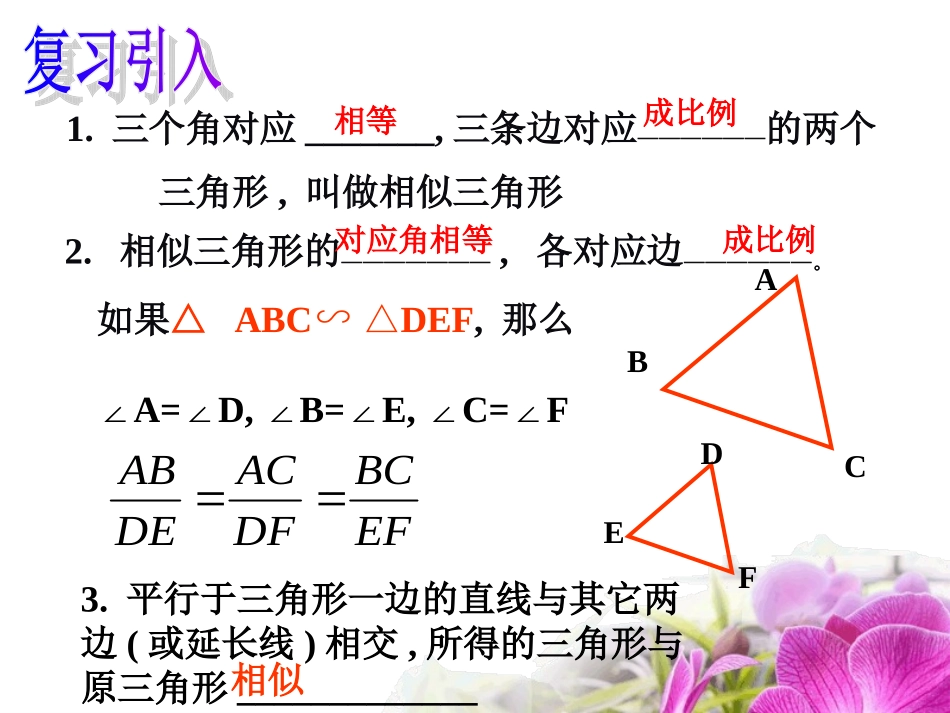
ABCDEF1.三个角对应_______,三条边对应——————的两个三角形,叫做相似三角形相等成比例2.相似三角形的———————,各对应边——————。对应角相等成比例如果△ABC∽DEF△,那么∠A=D,B=E,C=F∠∠∠∠∠EFBCDFACDEAB3.平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形_____________相似观察你与你同伴的直角三角尺,同样角度(30°与60°,或45°与45°)的三角尺看起来是相似的.这样从直观来看,一个三角形的三个角分别与另一个三角形的三个角对应相等时,它们就“应该”相似了.确实这样吗?•你认为判定两个三角形相似至少需要哪些条件你认为判定两个三角形相似至少需要哪些条件??•因为两个三角形相似仅仅是大小的不同因为两个三角形相似仅仅是大小的不同,,也就是边按也就是边按一定的比例放大或缩小一定的比例放大或缩小,,而角的大小与边的长短无关而角的大小与边的长短无关,,所以类比三角形全等可知…所以类比三角形全等可知…•如果两个三角形有若干个角对应相等会相似吗?如果两个三角形有若干个角对应相等会相似吗?演示相似演示相似演示相似演示相似判定三角形相似的方法之一判定三角形相似的方法之一•两角对应相等的两个三角形相似.这是一个今后经常用来判定两个三角形相似的重要方这是一个今后经常用来判定两个三角形相似的重要方法法,,务必予以熟练掌握务必予以熟练掌握..用数学符号表示:用数学符号表示:如图,在△ABC和△DEF中∵∠A=A∠',∠B=B∠'∴ΔABCΔA∽'B'C'CC'BB'AA'ABCA’C’B’下列图形中两个三角形是否相似?ABCDEABCA’B’C’ABCDE结论:只有一个角对应相等时,结论:只有一个角对应相等时,不能判定两个三角形相似。不能判定两个三角形相似。每人画一个△ABC,使∠A=30°,与同伴交流两个三角形是否相似?能否再简便一些?有一对角对应相等的两个三角形相似吗?例1如图,在两个直角三角形△ABC和△A′B′C′中,∠B=∠B′=90°,∠A=∠A′,证明这两个三角形是否相似.证明:∵∠B=∠B′=90°(已知),∠A=∠A′(已知),C'B'A'CBA∴△ABC∽△A′B′C′(两组对应角分别相等的两个三角形相似)例2:如图,△ABC中,DEBC∥,EFAB∥,证明:△ADEEFC.∽△证明:∵DE∥BC(已知)∴∠AED=∠C(两直线平行,同位角相等),∴∠CEF=∠A.(两直线平行,同位角相等)∴△ADE∽△EFC.(两组对应角分别相等的两个三角形相似)又∵EF∥AB(已知)ABCDEF如果点D恰好是边AB的中点,那么点E是边AC的中点吗?DE和BC又有什么关系?1.请你来判断下面的话是否正确。•(1)有一对角相等的三角形一定相似。()•(2)有一对锐角相等的两个直角三角形一定相似。()•(3)有一对角相等的两个等腰三角形一定相似。()××∨(3)BCDEFA•2.(2012•郴州)如图,D、E分别是△ABC的边AB、AC上的点,连结DE,要△ADEACB∽△,还需添加一个条_________.(只需写一个).3.在△ABC与△A′B′C′中,A∠=∠A′=50°,∠B=70°,∠B′=70°,这两个三角形相似吗?ABCA′B′C′变式一:如图,直线a、直线b相交于点A,点B、C分别在直线a、直线b上,在直线a、直线b上分别找两点D、E,使△BAC与△DAE相似,请尽量多地画出点D、E的位置。bABCa拓展思维ABCDEABCDEABCDABCDEbABCa“A”型ABCDE“共角”型“共边共角”型“X”型“蝴蝶”型变式二:1、根据条件指出下列图形中的相似三角形,并写出理由。CABDABCDE四边形ABCD,ADBC,A=90∥∠,BDD⊥C条件:B=D∠∠∠ACD=ABC∠CABD123回味无穷•判定三角形相似的常用方法:•如图,在△ABCD△中•如果∠A=D,B=E,∠∠∠•那么△ABCDEF.∽△ABC1.两角对应相等的两个三角形相似.DEF2.我们在运用上述判定两个三角形相似时,需要注意图中隐含的哪些条件?等角的余角、补角公共角对顶角直角两直线平行时的同位角、内错角我们在运用条件一判定两个三角形相似时,需要注意图中隐含的哪些条件?等角的余角、补角公共角对顶角直角两直线平行时的同位角、内错角