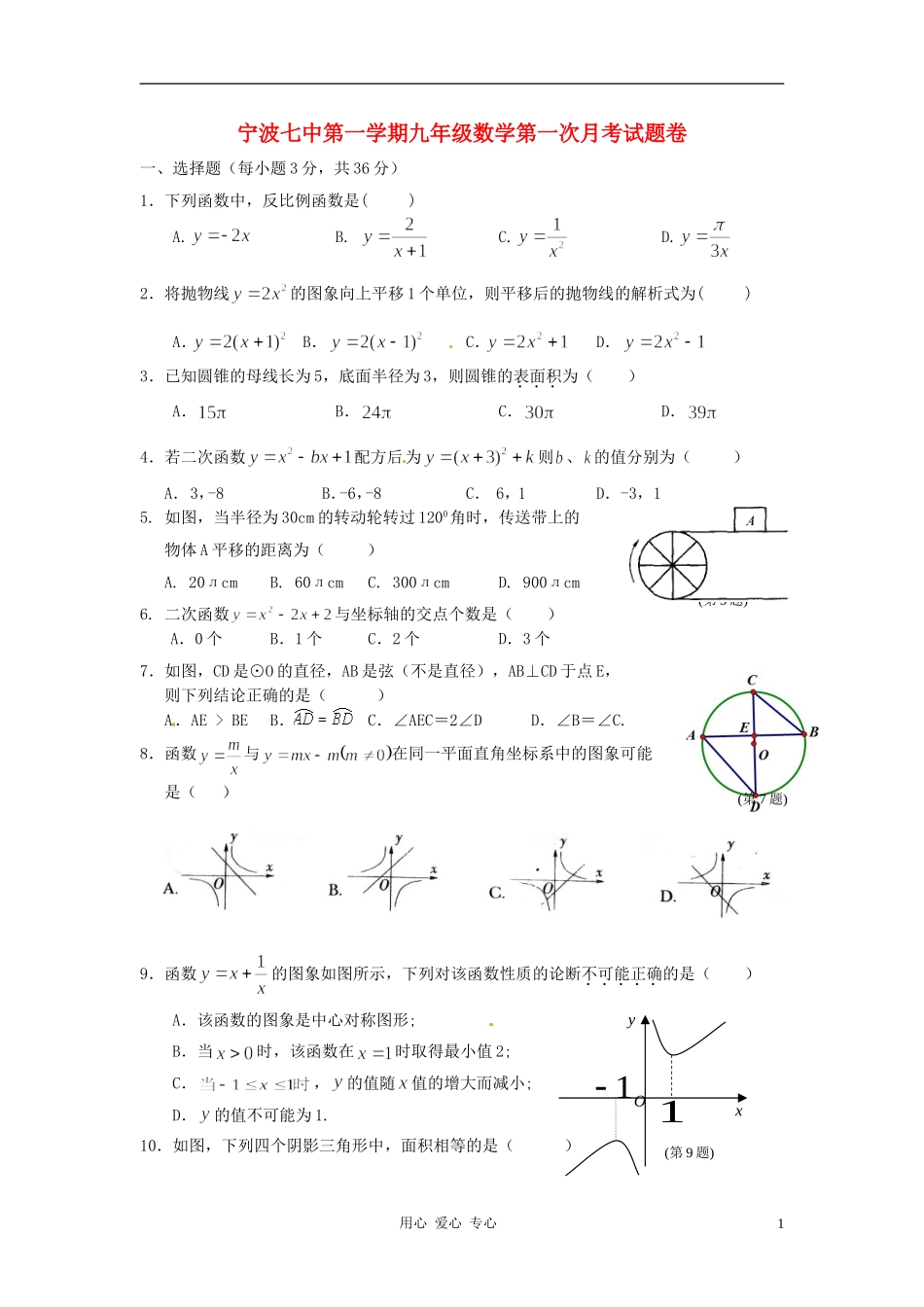
宁波七中第一学期九年级数学第一次月考试题卷一、选择题(每小题3分,共36分)1.下列函数中,反比例函数是()A.B.C.D.2.将抛物线的图象向上平移1个单位,则平移后的抛物线的解析式为()A.B.C.D.3.已知圆锥的母线长为5,底面半径为3,则圆锥的表面积为()A.B.C.D.4.若二次函数配方后为则、的值分别为()A.3,-8B.-6,-8C.6,1D.-3,15.如图,当半径为30cm的转动轮转过1200角时,传送带上的物体A平移的距离为()A.20лcmB.60лcmC.300лcmD.900лcm6.二次函数与坐标轴的交点个数是()A.0个B.1个C.2个D.3个7.如图,CD是⊙O的直径,AB是弦(不是直径),AB⊥CD于点E,则下列结论正确的是()A.AE>BEB.C.∠AEC=2∠DD.∠B=∠C.8.函数与在同一平面直角坐标系中的图象可能是()9.函数的图象如图所示,下列对该函数性质的论断不可能正确的是()A.该函数的图象是中心对称图形;B.当时,该函数在时取得最小值2;C.,的值随值的增大而减小;D.的值不可能为1.10.如图,下列四个阴影三角形中,面积相等的是()用心爱心专心1(第9题)yxO11(第5题)(第7题)11.已知抛物线,当自变量取两个不同的数值时,函数值相等,则当自变量取时的函数值与()A.时,函数值相等B.时,函数值相等C.时,函数值相等D.时,函数值相等12.已知正方形内接于半径为20,圆心角为的扇形(即正方形的各顶点都在扇形边或弧上),则正方形的边长是()A.B.C.或D.或二、填空题(每小题3分,共18分)13.抛物线的顶点坐标是______________.14.如图,C,D是以AB为直径的半圆周的三等分点,CD=8cm.则阴影部分的面积是_______.15.函数y=-的图象的两个分支分布在第_______象限.16.已知中,斜边AB=13cm,以直线BC为轴旋转一周,得到一个侧面积为65的圆锥,则BC=_______cm.17.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:从上表可知,下列说法中正确的有______.(填写序号)①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是x=;④在对称轴左侧,y随x的增大而增大.18.如图,□ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),顶点C,D在双曲线y=上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k=__________.用心爱心专心2(第14题)三、解答题(第19-21题各6分,第22-23题各8分,第24-25题10分,第26题12分,共66分)19.已知直角中,∠C=90°.(1)请用直尺和圆规在图中画出直角的外接圆;(不写作法,保留作图痕迹)(2)若AC=5,BC=12,请求出该直角的外接圆面积.20.已知反比例函数.(1)直接写出这个函数的比例系数____________;(2)求当x=-10时函数y的值;(3)求当y=6时自变量x的值.21.已知抛物线y=x2+x-.(1)求它的顶点坐标和对称轴;(2)若该抛物线与x轴的两个交点为A、B,求线段AB的长.22.如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上一点(不与点A、B重合),连结CO并延长CO交⊙O于点D,连结AD.(1)求弦长AB的长度;(结果保留根号);(2)当∠D=20°时,求∠BOD的度数.23.已知用圆心角为120°,面积为的扇形卷成一个无底圆锥形筒.(1)求这个圆锥形筒的高;用心爱心专心3(第19题)(第18题)ABC(第22题)(2)一只蚂蚁要从圆锥底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC的中点D,问蚂蚁沿怎样的路线爬行,使路程最短?最短路程是多少?24.如图,正比例函数的图象与反比例函数在第一象限的图象交于点,过点作轴的垂线,垂足为,已知的面积为1.(1)求反比例函数的解析式;(2)当x>0时,根据图象直接写出不等式>的解;(3)如果为反比例函数在第一象限图象上的点(点与点不重合),且点的横坐标为1,在轴上求一点,使最小.25.如图,用长为32米的篱笆围成一个外形为矩形的花圃,花圃的一边利用原有墙,中间用2道篱笆割成3个小矩形.已知原有墙的最大可利用长度为15米,花圃的面积为S平方米,平行于原有墙的一边BC长为x米.(1)求S关于x的函数关系式;(2)当围成的花圃面积为60平方米时,求AB的长;(3)能否围成面积比60平方米更大的花圃?如果能,那么最大的面积是...