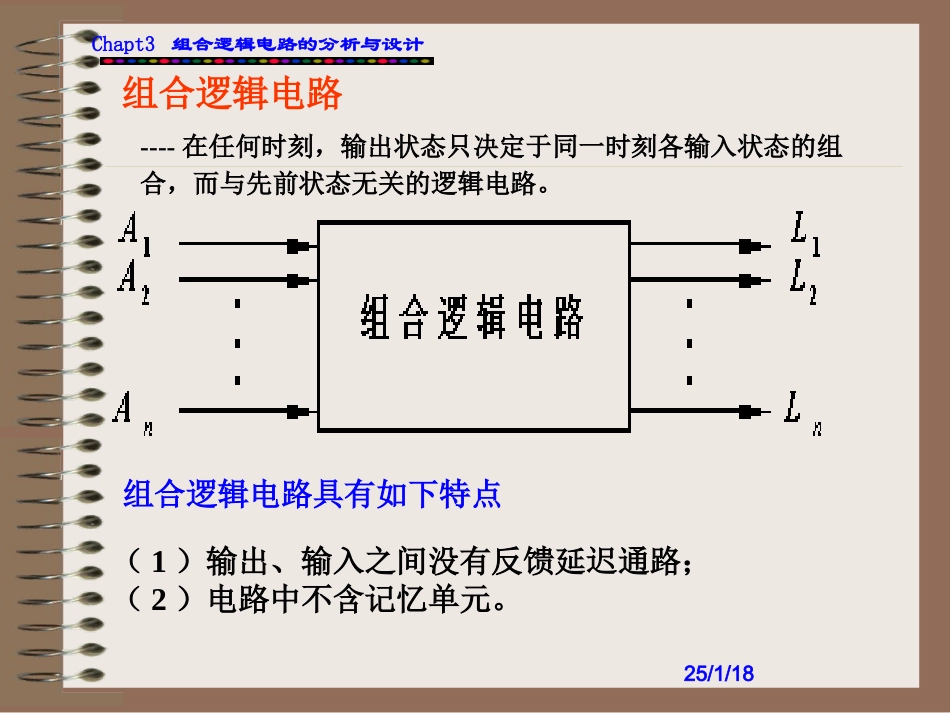
25/1/18Chapt3组合逻辑电路的分析与设计第三章组合逻辑电路的分析与设计[教学要求]1.掌握逻辑代数的三种基本运算、三项基本定理、基本公式和常用公式;2.掌握逻辑函数的公式化简法和卡诺图化简法;3.了解最小项、最大项、约束项的概念及其在逻辑函数化简中的应用;4.掌握组合逻辑电路的分析与设计方法;5.了解组合电路中的竞争与冒险现象、产生原因及消除方法。25/1/18Chapt3组合逻辑电路的分析与设计组合逻辑电路----在任何时刻,输出状态只决定于同一时刻各输入状态的组合,而与先前状态无关的逻辑电路。组合逻辑电路具有如下特点(1)输出、输入之间没有反馈延迟通路;(2)电路中不含记忆单元。25/1/18Chapt3组合逻辑电路的分析与设计3.1逻辑代数逻辑代数的基本定律和恒等式25/1/18Chapt3组合逻辑电路的分析与设计25/1/18Chapt3组合逻辑电路的分析与设计1.代入规则:在任何一个逻辑等式中,如果将等式两边出现的某变量A,都用一个函数代替,则等式依然成立。2.反演规则:求一个逻辑函数L的非函数时,可以将L中的与(·)换成或(+),或(+)换成与(·);再将原变量换为非变量(如A换成),非变量换为原变量;并将1换成0,0换成1;那么所得的逻辑函数式就是。注意事项:1)保持原来的运算优先顺序。2)对于反变量以外的非号应保留不变。3.对偶规则:如把L中的与(·)换成或(+),或(+)换成与(·);1换成0,0换成1,那么就得到一个新的逻辑函数,这就是L的对偶式,记作(L')。变换时仍需注意保持原式中先“与”后“或”的顺序。ALL三种规则:25/1/18Chapt3组合逻辑电路的分析与设计逻辑函数的代数变换与化简法1.逻辑函数的变换一个特定的逻辑问题,对应的真值表是唯一的,但实现它的电路多种多样。2.逻辑函数的化简:1)最简与或表达式有以下两个特点:a)与项(即乘积项)的个数最少。b)每个乘积项中变量的个数最少。2)方法:a)代数法。b)卡诺图法。3)代数法:并项法吸收法消去法配项法25/1/18Chapt3组合逻辑电路的分析与设计逻辑函数的卡诺图化简法一.最小项的定义及其性质:1.最小项:n个变量x1,x2….xn的最小项是n个因子的乘积,每个变量都以它的原变量或非变量的形式在乘积项中出现,且仅出现一次。2.最小项的性质:3.最小项的编号:二.逻辑函数的最小项表达式:任一个逻辑函数都可化成最小项表达式.三.用卡诺图表示逻辑函数:1.卡诺图:将函数的最小项表达式中的各最小项填入一个特定的方格中。25/1/18Chapt3组合逻辑电路的分析与设计ABC0000010100111001011101111000000001000000001000000001000000001000000001000000001000000001CBACBACBABCACBACBACABABC表3.2.13变量最小项真值表25/1/18Chapt3组合逻辑电路的分析与设计25/1/18Chapt3组合逻辑电路的分析与设计2.n个变量的逻辑函数有2n个最小项。3.卡诺图的特点:4.卡诺图的简化表示法:0000对应于,1111对应于ABCD,依类推。5.已知逻辑函数画卡诺图:四.用卡诺图化简逻辑函数:1.化简的步骤:1)将逻辑函数的项填入卡诺图(方格中填1)。2)在卡诺图上圈出全部最大相邻项,(包括圈内的方格数)必定是2n个,n等于0,1,2,3,…..;相邻方格包括上下底相邻,左右边相邻邦和四角相邻;同一方格可以被不同的包围圈重复包围,但新增包围圈中一定要有新的方格,否则该包围圈为多余;包围圈内的方格数要尽可能多,包围圈的数目要尽可能少。DCBA25/1/18Chapt3组合逻辑电路的分析与设计3)合并最小项。(如果有2n个最小项相邻,n=0,1,2,3,…..n,并排成一个矩形组,则它们可以合并为一项,并消去n对因子。合并后的结果中仅包含这些最小项的公共因子。五.例题.组合逻辑电路的分析一.目的:确定已知电路的逻辑功能.二.步骤:1)由逻辑图写出各输出端的逻辑表达式.2)化简和变换各逻辑表达式.3)列出真值表.4)根据真值表和逻辑表达式对逻辑电路进行分析,最后确定其功能.三.例题.25/1/18Chapt3组合逻辑电路的分析与设计25/1/18Chapt3组合逻辑电路的分析与设计25/1/18Chapt3组合逻辑电路的分析与设计输入输出ABSC0001101100101001表3.3.2例3.3.2表25/1/18Chapt3组合逻辑电路的分析与设计***例2:如图组合逻辑电路中,A、B为输入变量,S3、S2、S1、S0、为选择控制变量,F为输出函数。试写出电路在选择控制变量下的输出函数表达式...