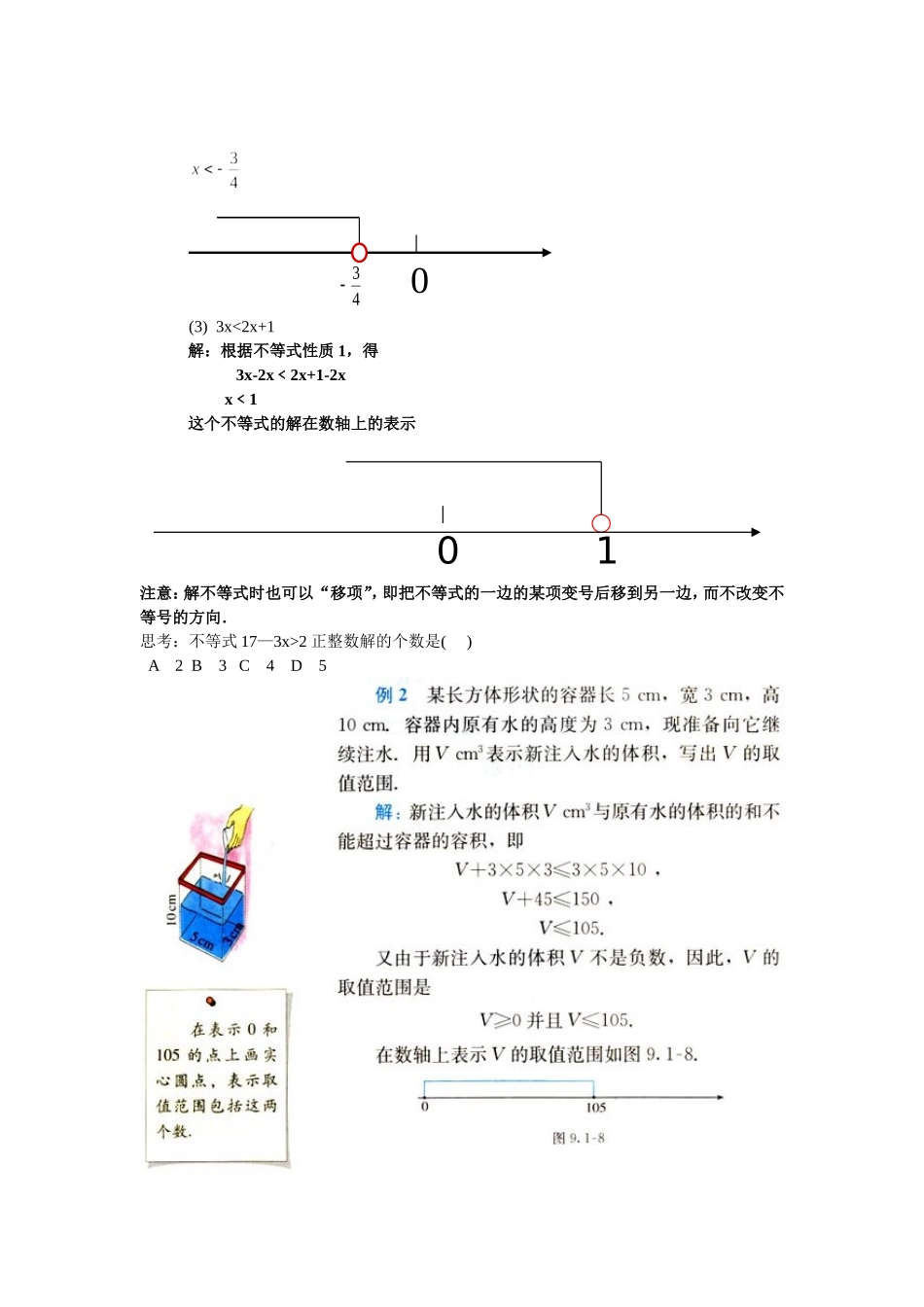
9.1.2.不等式的性质(2)教学目标1、进一步掌握不等式的三个基本性质;2、会运用不等式的性质解不等式教学重点、难点:重点:不等式的性质和解法.在实际问题中建立一元一次不等式的数量关系。难点:根据实际问题建立一元一次不等式教学过程:一、复习练习:1.叙述不等式的性质。2.填一填如果a>b,那么:①a—3__b—3,(不等式的性质_____)②2a____2b,(不等式的性质_____)③—3a____—3b(不等式的性质_____)④a—b____0(不等式的性质_______)3.练一练A1、如果x+5>4,那么两边都可得x>-1B2、在x-7<8的两边都加上7可得。C3、在x+5>-2的两边都减去5得。D4、在-3x>-4的两边都除以—3可得。二、新授课:例题讲解例1利用不等式的性质解下列不等式用数轴表示解集•(1)x-7>26(解:根据不等式性质1,得x-7+7>26+7x>33)(1)-4x﹥3解:根据不等式性质3,得330(3)3x<2x+1解:根据不等式性质1,得3x-2x﹤2x+1-2xx﹤1这个不等式的解在数轴上的表示注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.思考:不等式17—3x>2正整数解的个数是()A2B3C4D504301三、巩固提高1用不等式的性质解下列不等式并在数轴上表示解集:(1)(2)(3)(4)2.用不等式表下列语句并写出解集,并在数轴上表示解集:(1)x的3倍大于或等于1;(2)x与3的和不小6;(3)a与b的和大于或等于83.思考A是任意有理数,试比较5a与3a的大小四、课堂小结本节课你有哪些收获.五、课后作业:课本P120的3题、5题