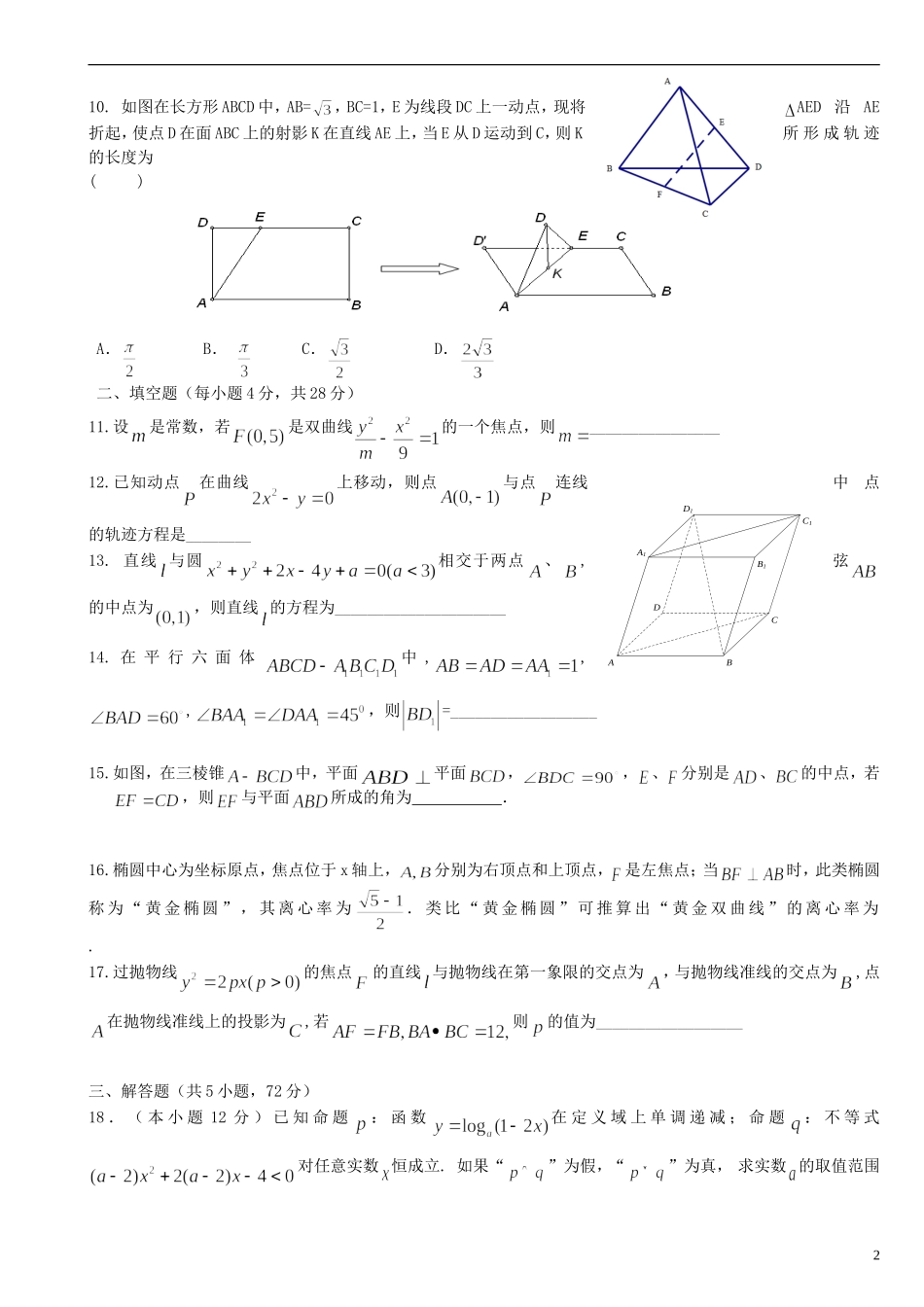
2012学年第一学期高二第三次月考理科数学试题卷一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.“”是“直线和直线互相平行”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.设为两条直线,为两个平面,下列四个命题中,真命题为()A.若与所成角相等,则B.若,则C.若,则D.若,则3.一个棱长为2cm的正方体的顶点都在球面上,则此球的表面积是()A.B.C.D.4.若一个组合体的三视图如图所示,则这个组合体的体积为()A.B.C.D.5.已知直线和直线相互垂直,则的值为()A.B.C.D.或6.若椭圆和双曲线有相同的焦点和,而是这两条曲线的一个交点,则的值是()A.B.C.D.7.已知正方体的棱长为1,若点在正方体的内部且满足:,则点到直线的距离为()A.B.C.D.8.直线与圆相交于两点,若,则的取值范围是()A.B.C.D.9.设F是抛物线02:21ppxyC的焦点,点A是抛物线1C与双曲线1:22222byaxC0,0ba的一条渐近线的一个公共点,且AFx轴,则双曲线的离心率为()A.25B.5C.3D.2122俯视图侧视图主视图210.如图在长方形ABCD中,AB=,BC=1,E为线段DC上一动点,现将AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为()A.B.C.D.二、填空题(每小题4分,共28分)11.设是常数,若是双曲线的一个焦点,则________________12.已知动点在曲线上移动,则点与点连线中点的轨迹方程是________13.直线与圆相交于两点、,弦的中点为,则直线的方程为_____________________14.在平行六面体中,,,,则=__________________15.如图,在三棱锥中,平面平面,,、分别是、的中点,若,则与平面所成的角为.16.椭圆中心为坐标原点,焦点位于x轴上,分别为右顶点和上顶点,是左焦点;当时,此类椭圆称为“黄金椭圆”,其离心率为.类比“黄金椭圆”可推算出“黄金双曲线”的离心率为.17.过抛物线的焦点的直线与抛物线在第一象限的交点为,与抛物线准线的交点为,点在抛物线准线上的投影为,若则的值为__________________三、解答题(共5小题,72分)18.(本小题12分)已知命题:函数在定义域上单调递减;命题:不等式对任意实数恒成立.如果“”为假,“”为真,求实数的取值范围2第12题B1C1D1A1DCBA19.(本小题15分)在直三棱柱中,,,E是BC的中点,G是的中点,求:(1)异面直线AE与所成角的大小(2)直线AC与平面AGE所成角的正弦值(3)求到平面AEG的距离20.(本小题15分)已知过抛物线的焦点,斜率为的直线交抛物线于,两点,且.(1)求该抛物线的方程;(2)为坐标原点,是否存在平行于的直线,使得直线与抛物线有公共点,且直线与的距离为?若存在,求出直线的方程;若不存在,说明理由.21.(本小题15分)如图,已知四棱锥底面为菱形,平面,、分别是、的中点.(1)证明:(2)设AB=2,若为线段上的动点,与平面所成的最大角的正切值为求二面角的余弦值.22.(本小题15分)在椭圆中,为椭圆上的一点,过坐标原点的直线交椭圆于两点,其中在第一象限,过作轴的垂线,垂足为,连接,(1)若直线与的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;(2)若为的延长线与椭圆的交点,求证:.3育青中学2012学年第一学期高二第三次月考数学答题卷一、选择题题号12345678910答案二、填空题:11、12、13、14、15、16、17、三、解答题(共5小题,72分)18.(本小题12分)已知命题:函数在定义域上单调递减;命题:不等式对任意实数恒成立.如果“”为假,“”为真,求实数的取值范围19.(本小题15分)在直三棱柱中,,,E是BC的中点,G是的中点,求:(1)异面直线AE与所成角的大小(2)直线AC与平面AGE所成角的正弦值(3)求到平面AEG的距离4班级姓名学号考号20.(本小题15分)已知过抛物线的焦点,斜率为的直线交抛物线于,两点,且.(1)求该抛物线的方程;(2)为坐标原点,是否存在平行于的直线,使得直线与抛物线有公共点,且直线与的距离为?若存在,求出直线的方程;若不存在,说明理由.21.(本小题15分)如图,已知四棱锥底面为菱形,5平面,、分别是、的中点.(1)...