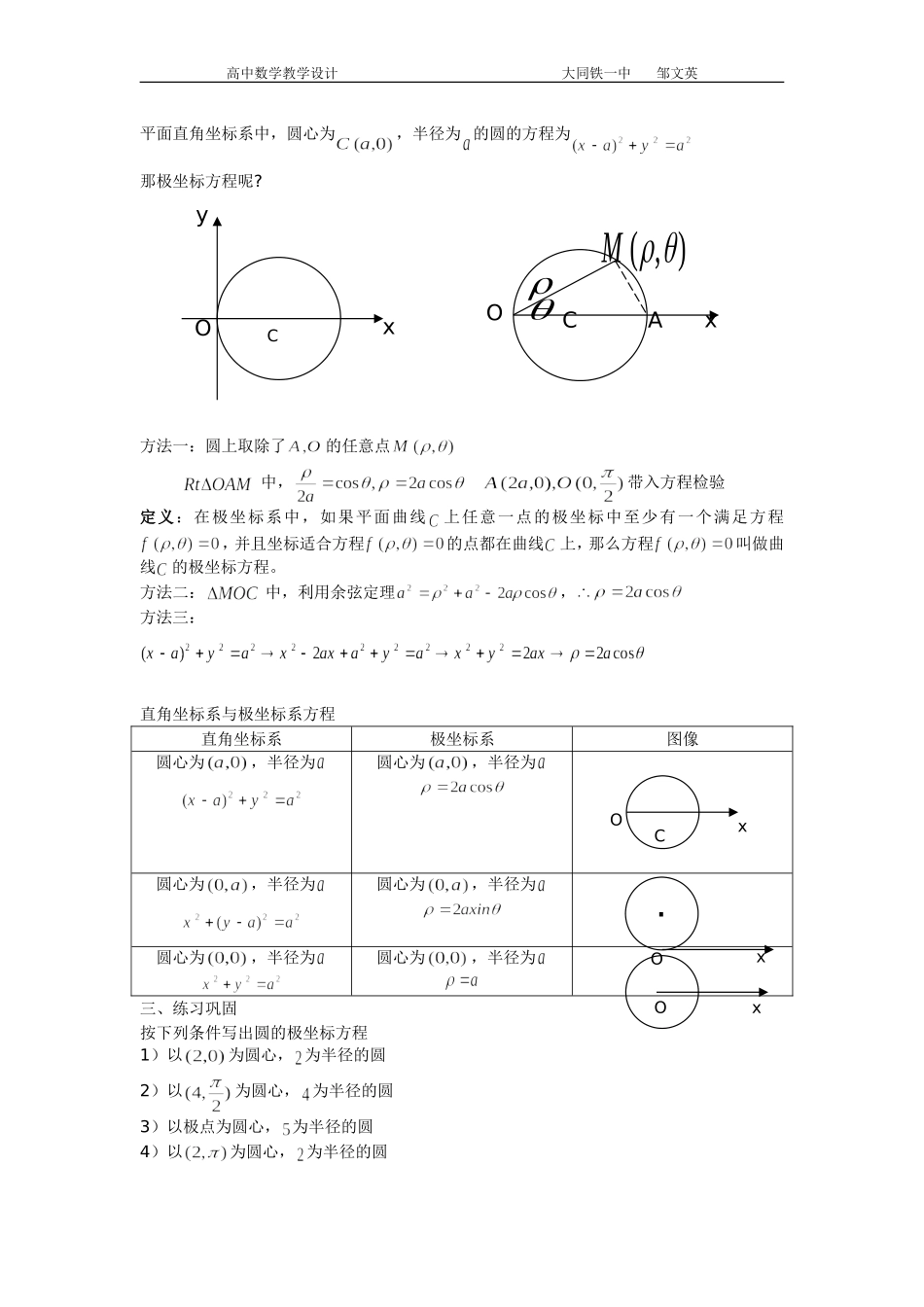
高中数学教学设计大同铁一中邹文英圆的极坐标方程教材分析:在平面直角坐标系中,平面曲线可以用方程表示。类似的,在极坐标系中,是否也可以用方程来表示平面曲线呢?因此,在引导学生回顾直角坐标系下曲线与方程关系的基础上,用类比的方式引进曲线的极坐标方程。学生分析:本班学生基础较好,学习的自觉性和主动性较强,有一定的自主学习和探究学习能力,平时的学习养成了善于观察、分析和思考的习惯,从而本节课从学生学习的角度来看不会存在太多的障碍,因而教学方法可以是引导学生自主的研究圆的极坐标方程的建立。教学目标:一、知识目标1、会用两种方法求特殊位置的圆的极坐标方程2、理解极坐标方程的定义3、熟悉特殊位置的圆的极坐标方程二、能力目标1、掌握求曲线极坐标方程的方法2、掌握圆的极坐标方程与直角坐标方程的互化三、情感目标通过对圆的两种方程及其求解过程进行比较,体会两者之间的差异,从而加深对选择坐标系重要性的认识。教学重点:1、特殊位置的圆的极坐标方程2、圆的极坐标方程与直角坐标方程的互化教学难点:1、圆的极坐标方程的建立2、极坐标方程定义的理解教学措施:教师引导下的学生自主探究教学过程:一、复习引入1、求曲线方程的步骤:建系→设点→列式→化简2、极坐标与直角坐标的互化关系式:二、新课教学思考:高中数学教学设计大同铁一中邹文英平面直角坐标系中,圆心为,半径为的圆的方程为那极坐标方程呢?方法一:圆上取除了的任意点中,带入方程检验定义:在极坐标系中,如果平面曲线上任意一点的极坐标中至少有一个满足方程,并且坐标适合方程的点都在曲线上,那么方程叫做曲线的极坐标方程。方法二:中,利用余弦定理,方法三:直角坐标系与极坐标系方程直角坐标系极坐标系图像圆心为,半径为圆心为,半径为圆心为,半径为圆心为,半径为圆心为,半径为圆心为,半径为三、练习巩固按下列条件写出圆的极坐标方程1)以为圆心,为半径的圆2)以为圆心,为半径的圆3)以极点为圆心,为半径的圆4)以为圆心,为半径的圆OxOyCx),(MCOAxCxOxO高中数学教学设计大同铁一中邹文英5)以为圆心,为半径的圆四、典例分析例1、极坐标方程表示的曲线是()A直线B圆C双曲线D抛物线变式:极坐标方程表示的曲线是()A直线B圆C双曲线D抛物线例2、已知圆的极坐标方程为,圆心为,点的极坐标为,则为()ABCD变式:在极坐标系中,过点作圆的切线,为切点,求的长。例3、在极坐标系中,以为圆心,半径为的圆的方程为五、小结1、3种特殊位置的圆的极坐标方程2、怎样求圆的极坐标方程3、圆的极坐标方程的应用板书设计一、复习引入二、演算步骤1、求曲线方程的步骤建系→设点→列式→化简2、极坐标与直角坐标的互化关系式《圆的极坐标方程》教学反思像曲线的直角坐标方程一样,把曲线看成是动点的轨迹,那么极坐标方程就反映了曲线上动点的运动规律。曲线与其极坐标方程的关系,与曲线与其直角坐标方程的关系类似。由于与都有明确的几何特征,有些曲线所蕴含的运动规律用极坐标方程表示更简洁。本节课通过思考,要求学生写出半径为,过极点且圆心在极轴上的圆的极坐标方程。引导学生类比直角坐标系下求圆的方程的过程,先作出图形,再根据几何条件建立关于与的方程。这里提醒学生设为圆上除点以外的任一点,这样连接发现相应的几何关系,借助这种几何关系就比较容易建立曲线的方程。得到方程后还要验证的坐标也满足方程。方法二和方法一都是在三角形内利用边角关系列式得到方程。方法三是利高中数学教学设计大同铁一中邹文英用了曲线的极坐标方程与直角坐标方程互化关系式。三种方法的教学体现知识形成过程,使得学生的认知拓宽,思维方式多样。在思考的基础上例题的设置进一步提升,加深学生对极坐标方程的认识。教学的过程就是在教师的控制下的学生自主学习和合作探究学习的过程,这个过程中的关键点是怎么样有效地控制学生自主学习和合作探究学习的时间和空间。在教学的过程中,我较好地处理了学生学习的空间与时间,既留给学生充分思考和探索的时间与空间,又严格限定时间,由此培养学生思维的敏捷性,提高课堂效率。对于选编的例习题注意典型性,...