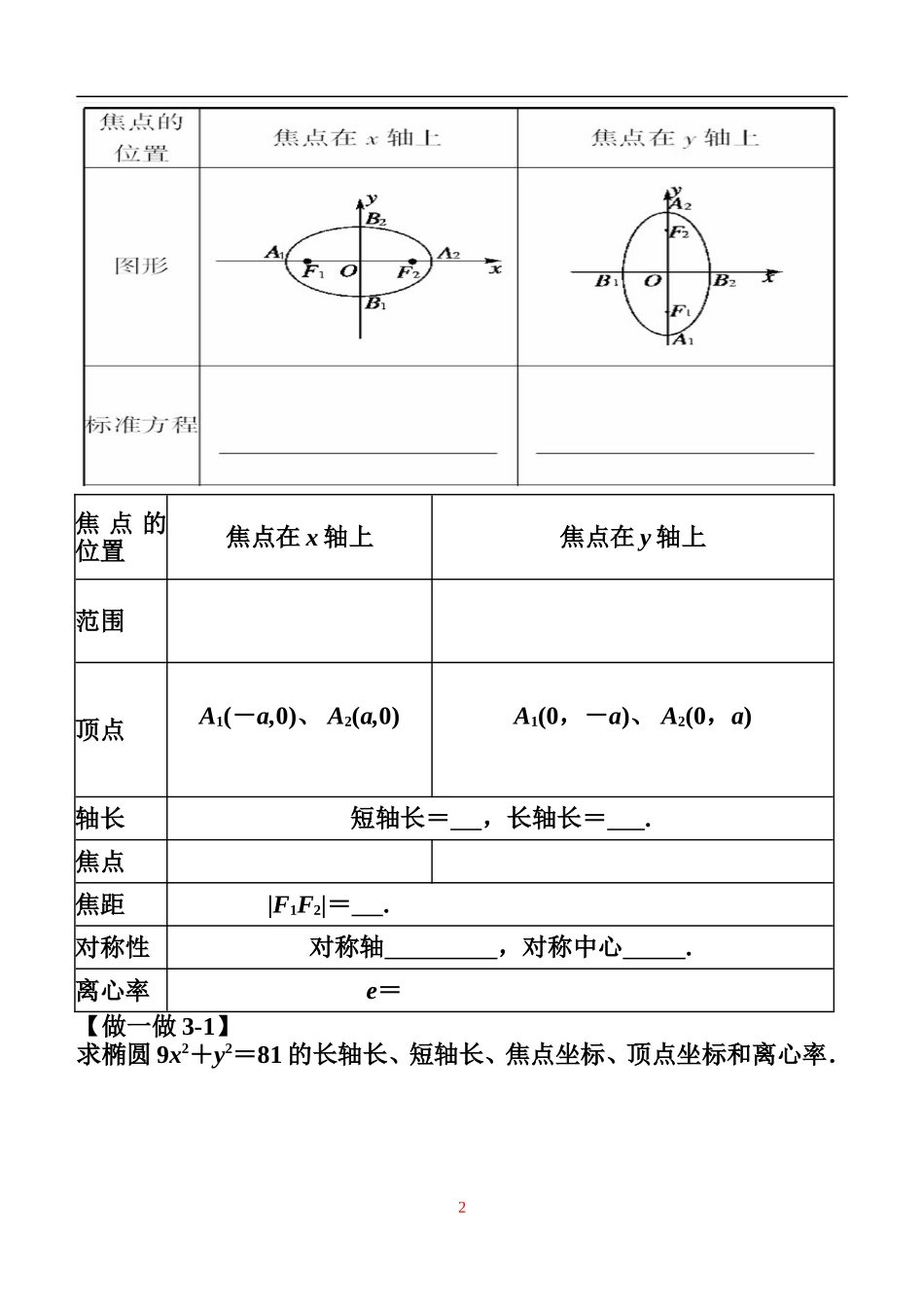
椭圆的标准方程及几何性质习题课学案复习回顾1.椭圆的定义平面内与两个定点F1,F2的_________等于常数(_________)的点的轨迹(或集合)叫做椭圆.这两个____叫做椭圆的焦点,______的距离叫做椭圆的焦距.※注意:在椭圆的定义中,(1)当常数等于|F1F2|时,动点的轨迹是__________.(2)当常数小于|F1F2|时,动点的轨迹_________.【做一做1-1】到两定点F1(-5,0)和F2(5,0)的距离之和为10的点M的轨迹是()A.椭圆B.线段C.圆D.以上都不对【做一做1-2】已知椭圆上一点P到椭圆两个焦点F1,F2的距离之和等于10,若椭圆上另一点Q到焦点F1的距离为3,则点Q到焦点F2的距离为()A.2B.3C.5D.7复习回顾2.椭圆的标准方程焦点在x轴上焦点在y轴上标准方程焦点坐标a,b,c的关系想一想:已知椭圆的标准方程,如何判断焦点在哪个轴上?【做一做2-1】【做一做2-2】求中心在原点,焦点在坐标轴上,且经过两点的椭圆的标准方程.复习回顾3.椭圆的几何性质1焦点的位置焦点在x轴上焦点在y轴上范围顶点A1(-a,0)、A2(a,0)A1(0,-a)、A2(0,a)轴长短轴长=,长轴长=.焦点焦距|F1F2|=.对称性对称轴,对称中心.离心率e=【做一做3-1】求椭圆9x2+y2=81的长轴长、短轴长、焦点坐标、顶点坐标和离心率.2【做一做3-2】若焦点在x轴上的椭圆+=1的离心率为,则m=()A.B.C.D.高考题链接1、(高考北京卷)椭圆+=1的焦点为F1,F2,点P在椭圆上.若|PF1|=4,则∠F1PF2的大小为________.2、(高考广东卷)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是()A.B.C.D.3.(高考全国卷Ⅱ)椭圆+=1(a>b>0)的左焦点为F1(-c,0),已知A(-a,0),B(0,b)是两个顶点,如果F1到直线AB的距离为,则椭圆的离心率e=________.3