三角函数复习VIP免费

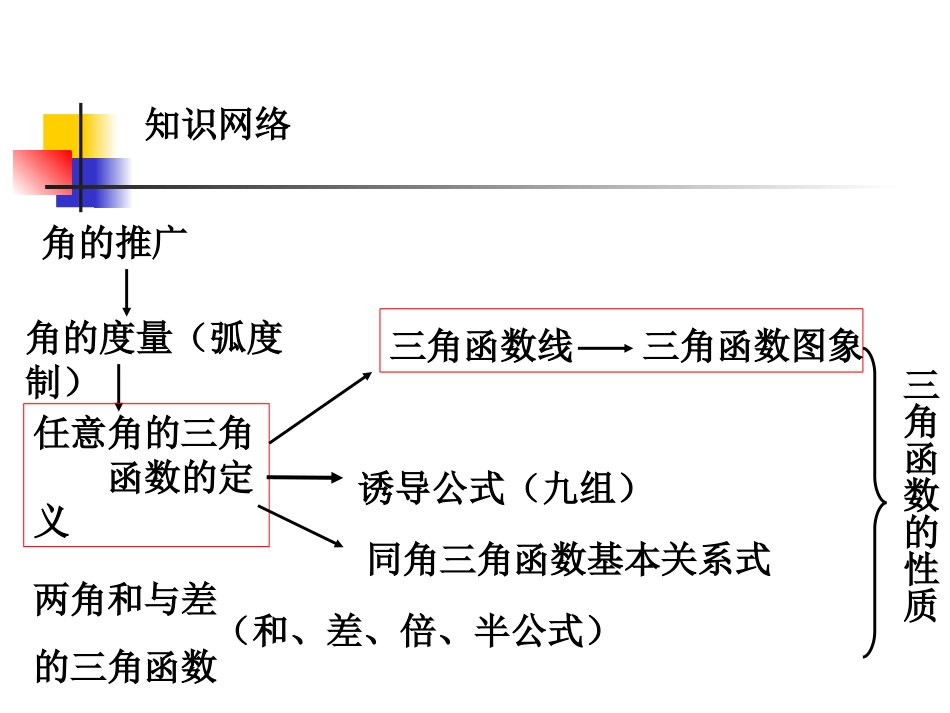
三角函数知识网络角的推广角的度量（弧度制）任意角的三角函数的定义同角三角函数基本关系式诱导公式（九组）三角函数线三角函数图象两角和与差的三角函数（和、差、倍、半公式）三角函数的性质高考要求（考什么）：1理解任意角的概念、弧度的意义；能正确地进行弧度与角度的换算。2掌握任意角的正弦、余弦、正切的定义，了解正割、余割的定义；掌握同角三角函数的基本关系式；掌握正弦、余弦的诱导公式；了解周期函数与最小正周期的意义。能运用上述公式进行简单三角函数式的化简、求值和恒等式证明。高考要求：3掌握两角和与两角差的正弦、余弦、正切公式；掌握二倍角的正弦、余弦、正切公式；通过公式的推导，了解他们的内在联系，从而培养逻辑推理能力。能正确运用上述公式进行简单三角函数式的化简、求值和恒等式证明。高考要求：4了解如何利用正弦线、正切线画出正弦函数、正切函数的图像，了解利用诱导公式由正弦函数的图像画出余弦函数的图像；并通过这些图像了解正弦、余弦、正切函数的性质；会用“五点法”画出正弦函数、余弦函数和y=Asin(bx+c)的简图。5会由已知三角函数值求角，并会用符号arcsinx,arccosx,arctanx表示.复习建议：把握复习难度：抓好基础、掌握通性通法数学思想方法：在三角函数（1）这一章中大量运用了“转化与化归”的思想。主要包括：把未知转化为已知；把特殊转化为一般，以及等价转化等。（2）还用到“数形结合”的思想、“分类讨论”的思想、“函数与方程”的思想。在三角函数式恒等变型中，化简最常见，其主要途径是：（1）降低式子的次数（常用半角公式）；（2）减少角的种类；（3）减少三角函数的种类。指导思想：注重大思路，淡化小技巧。基本方向是通过等价变形，努力造成合并、约分和特殊角。在运算能力上注意精算与估算结合、以图助算、列表分析等方法。总之，新课程高三复习内容多，课时紧，一定要把握复习的脉搏，抓住基础，敢于取舍，在120分之内下功夫。高考中三角函数的内容属于前88分（选择、填空和解答题的第一题），务必准确落实，确保不丢分。一角的概念1角的定义OAB2角的分类：（1）按旋转方向不同产生的角（2）直角坐标系中按终边位置终边相同的角象限角轴上角三角函数（1）3角的度量（1）角度制（2）弧度制把长度等于半径长的弧所对的圆心角叫做1弧度的角（3）角度制与弧度制的互化180抓住4三角函数的概念在直角坐标系中，设是一个任意角，的终边上任意一点P(x,y)，她与原点的距离是r,则xyrxrytancossin正切余弦正弦yxxryrcotseccsc余切正割余割P(x,y)xy0（1）定义（2）三角函数值的符号（3）特殊角的三角函数值5同角三角函数的基本关系式6诱导公式（9组）“奇变偶不变，符号看象限”练习1写出与-4200终边相同的角的集合其中最小的正角是练习2（1）写出终边落在OA上的角的集合（2）写出终边落在阴影部分角的集合OAB例1若是第三象限的角，试求的范围，并用单位圆表示。3,2例2（1）已知角的终边经过点A（-1，）求的值。（2）已知角的终边上一点B的坐标是（3a，4a)其中a<0，求的各三角函数值。tan,cos,sin3引例（94—18）43cot34tan.34tan,43tan,2524tan1tan2:,25242sincot),,0(,51cossin2故、估值可得由单位圆及三角函数线或可解出再由万能公式可得平方得：分析：由已知条件两边的值是则已知：注意知识之间的内在联系可有：.15122得到解决的一元二次方程，问题得关于，消转化为代数方程组问题xyyxyx可解再用若用71)4tan(,51)4sin(2例题选析（怎么考）例1（04—京9）函数分析：的最小正周期是xxxxfcossin322cos)(22)32cos(22sin32cos)(Txxxxf例2（04—京15）105,60451800,21)45cos(22)45cos(2cossin.tan,3,2,22cossinAAAAAAAABCAABACAAABC分析：的面积的值和求中，在应确保得满分。收性质，多，但是不难，具有验评：体现基础，知识点)62(434623221sin214...