相似三角形的判定定理2VIP免费

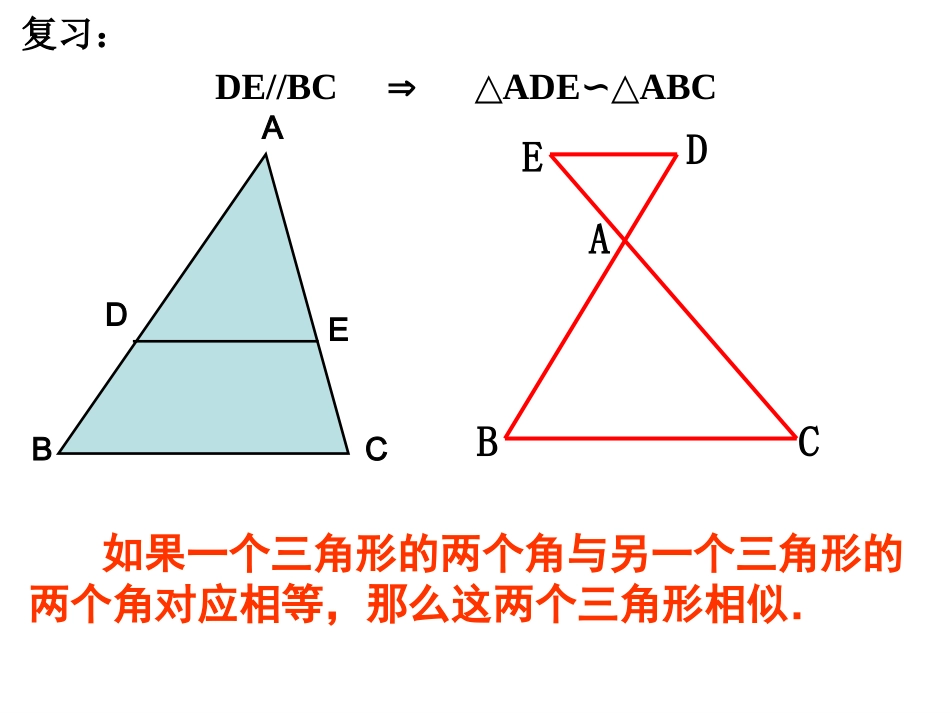
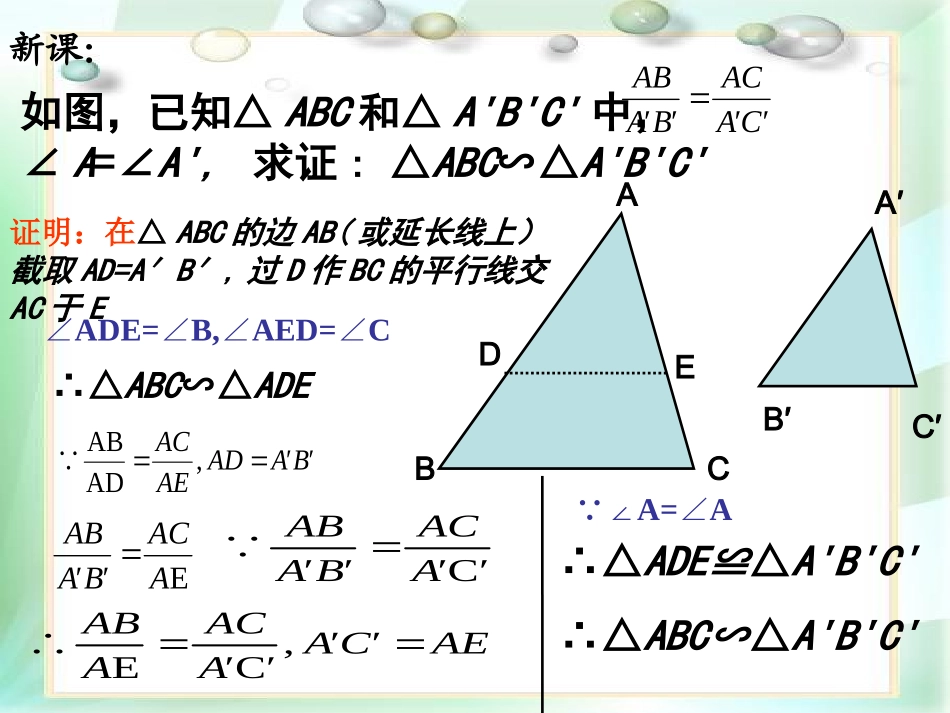
相似三角形的判定定理2复习：△ADEABC∽△DE//BCABCDEADBCE如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似．新课：∠ADE=∠B,∠AED=∠C证明：在△ABC的边AB(或延长线上）截取AD=A′B′,过D作BC的平行线交AC于E如图，已知△ABC和△A'B'C'中，∠A=∠A',求证:△ABC∽△A'B'C'′′′′CAACBAABABCDEA′B′C′∴△ABC∽△ADE′′,ADAB∵BAADAEACE′′AACBAAB′C′′′∵AACBAABAECAAACAAB′′,′C′E∴∵∠A=∠A∴△ADE≌△A'B'C'∴△ABC∽△A'B'C'由此我们可以归纳一个定理：相似三角形判定定理2：如果一个三角形的两边与另一个三角形的两边对应成比例,并且相应的夹角相等,那么这两个三角相似.例1:根据下列条件，判断△ABC与△A’B’C’是否相似，并说明理由．(1)A=120∠0,AB=7cm,AC=14cm.∠A’=1200,A’B’=3cm,A’C’=6cm.''',''.''',37614'',37''∵)1(:CBAABCAACAACBAABCAACBAAB∽解：1.已知：如图，在正方形ABCD中，P是BC上的点，且BP=3PC，Q是CD的中点.ΔADQ与ΔQCP是否相似？为什么？2如图，ABAE=ADAC••，且∠1=∠2，求证：△ABC∽△AED．21EDCBA3.已知：如图，P为△ABC中线AD上的一点，且BD2=PD×AD求证：△ADC∽△CDP．PDCBA