相似三角形复习课件VIP免费

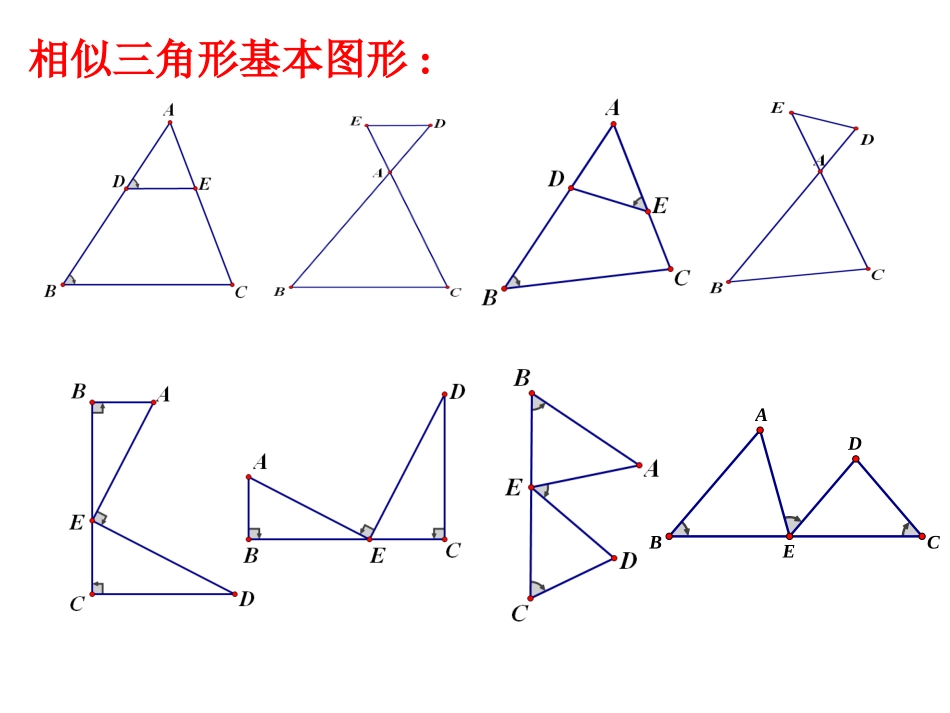
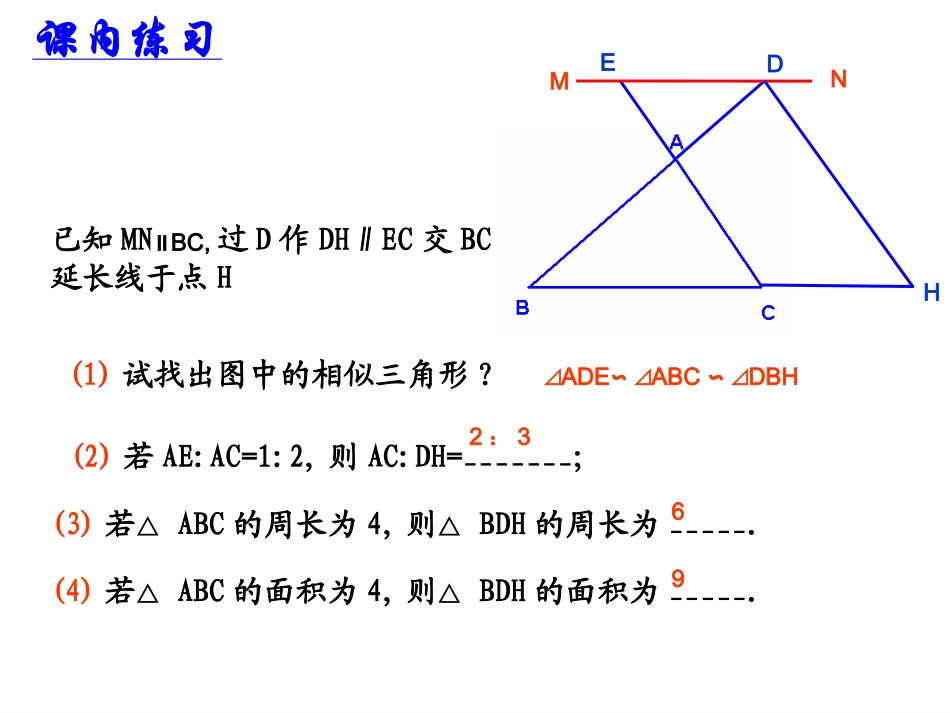
相似三角形基本图形:BCADE课内练习DEMNH已知MNBC,∥过D作DH∥EC交BC延长线于点H(1)试找出图中的相似三角形?(2)若AE:AC=1:2,则AC:DH=_______;(3)若△ABC的周长为4,则△BDH的周长为_____.(4)若△ABC的面积为4,则△BDH的面积为_____.⊿ADEABCDBH∽⊿∽⊿2：3692.如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则DF：FC=（）A．1：4B．1：3C．2：3D．1：2课内练习3如图M是直角△ABC的斜边BC上异于B,C的一定点，过点M作直线截△ABC，使截得的三角形与△ABC相似，这样的直线共有（）A1条B2条C3条D4条ABCM．课内练习•4、如图，梯形ABCD中，AD∥BC，AC与BD相交于点O，过B点作BE∥CD交CA的延长线于点E．求证：OC2=OA·OECDAOBEPCBAQ在Rt△ABC中,∠C=900,AC=3cm,BC=4cm,如果P、Q分别是AB、BC上的动点，点P从点B出发，点Q从点A出发，并且两点同时出发，速度都是1cm/秒，连结PQ。问：经过几秒后，使得△BPQ与△ABC相似？请说明理由。3cm4cmPCBAQ解：Rt△ABC中,AB=AC2+BC2=32+42=5cm设BP=AQ=t(1)当PQAC∥时，△QBP∽△ABC ⊿QBPABC∽⊿∴BP:BC=BQ:BA∴t:4=(5－t):5∴9t=20∴t=20/93cm4cm5cmPCBAQ(2)当PQAB⊥时，△PBQ∽△ABC △PBQ∽△ABC∴BP:AB=BQ:BC∴t:5=(5－t):4∴9t=25∴t=25/9综上所述，经过20/9或25/9秒后，使得△BPQ与△BAD相似2.如图,在直角梯形ABCD中,ABCD,A=90∥∠0,AB=2,AD=5,P是AD上一动点(不与A、D重合),ＰＥ⊥ＢＰ，ＰＥ交ＤＣ于点Ｅ．(1)ABP△与△DPE是否相似？请说明理由；(2)设ＡＰ＝xＤＥ=y，求y与x之间的函数关系式,并指出自变量x的取值范围；(3)请你探索在点P运动的过程中，四边形ABED能否构成矩形？如果能，求出AP的长；如果不能，请说明理由；(4)当点P运动到何处时四边形ABED的面积最大？求出此时AP的长(5)当点P运动到何处时,ABPPBE△∽△？求出此AP的长ECABDP这类题型的特征：有条件而无结论，要确定这些条件下可能出现的结论．解题思路是：从所给条件出发，通过分析、比较、猜想、寻求多种解法和结论，再进行证明.如图，已知：ABDB⊥于点B，CDDB⊥于点D，AB=6，CD=4，BD=14.问：在DB上是否存在P点，使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似相似？如果存在，计算出点P的位置；如果不存在，请说明理由。4614ADCB解（1）假设存在这样的点P，使△ABPC∽△DP设PD=x，则PB=14―x，∴6：4=（14―x）:x则有AB:CD=PB:PD∴x=5.6P6x14―x4ADCBP（2）假设存在这样的点P,使△ABPPDC,∽△则则有AB:PD=PB:CD设PD=x，则PB=14―x，∴6：x=（14―x）:4∴x=2或x=12∴综上所述，当PD的长为2或12或5.6时，以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似46x14―xDBCAp1、如图,在等腰△ABC中,BAC=90°,AB=AC=1,∠点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°（1）求证：△ABDDCE∽△（2）设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围，并求出当BD为何值时AE取得最小值（3）当△ADE是等腰三角形时，求AE的长CABDE巩固练习：巩固提高：在∆ABC中，AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动，点Q从点B开始沿BC向点C以4cm/秒的速度移动，如果P、Q分别从A、B同时出发，经几秒钟∆BPQ与∆BAC相似？分析：由于∆PBQ与∆ABC有公共角∠B；所以若∆PBQ与∆ABC相似，则有两种可能一种情况为,即PQAC;∥另一种情况为CBQBABPBABQBCBPBBCAQP8162cm/秒4cm/秒如图所示,有一边长为5cm的正方形ABCD和等腰⊿PQR,PQ=PR=5cm,QR=8cm,点B、C、Q、R在同一直线上,从C、Q两点重合时，等腰⊿PQR以1cm/s的速度沿直线按箭头所示方向开始匀速运动，t(s)后正方形ABCD与等腰⊿PQR重合部分为S（cm2）(C)BDPAQR⑴当t=3时，求的S值55585CBDPAQRGE⑴当t=3时，求的S值334解:如图(1)作PEQR,E⊥为垂足 PQ=PR∴QE=RE=1/2QR=4cm∴由勾股定理，得PE=3cm当t=3时，QC=3,设PQ与DC交于点G PEDC∥∴⊿QCGQEP∽⊿∴S:SQEP⊿=(3/4)2 SQEP⊿=1/2×4×3=6∴S=(3/4)2×6=27/8（cm2）⑵当t=5时，求的S值CBDPAQRGE34⑵如图，当t=5时，CR=3,设PR与DC交于点G PEDC∥∴⊿RCGREP∽⊿同理，得SRGC⊿=27/8（c...