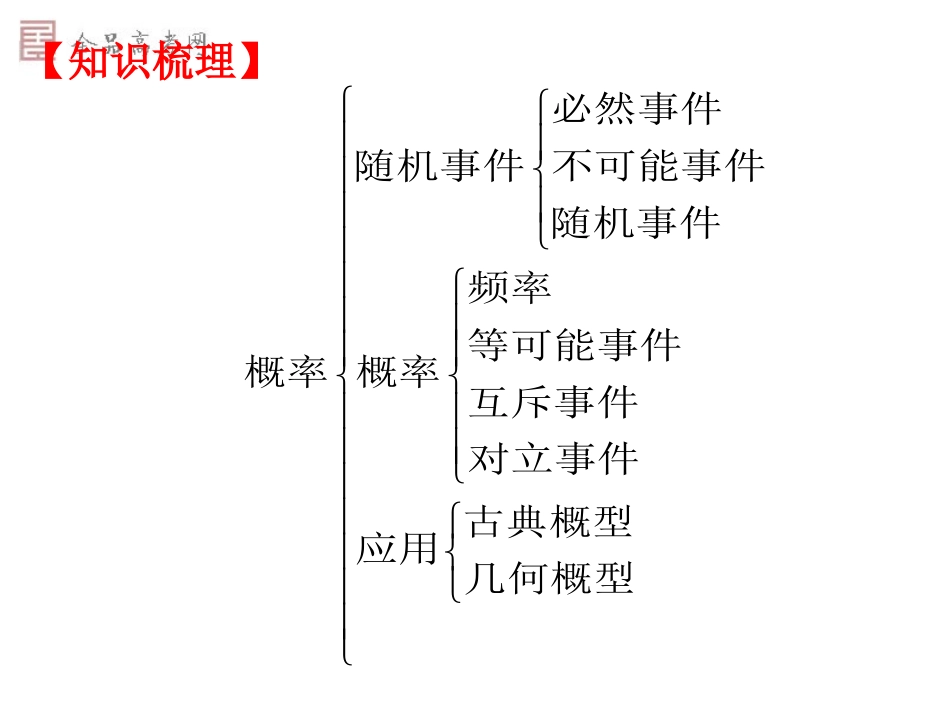
概率复习概率复习考点:1、频率与概率的意义2、古典概型3、几何概型4、互斥事件和对立事件必然事件随机事件不可能事件随机事件频率等可能事件概率概率互斥事件对立事件古典概型应用几何概型【知识梳理】古典概型的特点:(1)试验中所有可能出现的基本事件只有有限个;(2)每个基本事件出现的可能性相等。P(A)=A包含的基本事件的个数基本事件的总数几何概型的特点:(1)试验中所有可能出现的结果(基本事件)有无限多个.(2)每个基本事件出现的可能性相等.P(A)=构成事件A的区域长度(面积或体积)试验的全部结果所构成的区域长度(面积或体积)例1:判断下列给出的事件是否为互斥事件,是否为对立事件,并说明道理.从40张扑克牌(红桃,黑桃,方块,梅花点数从1~10各10张)中,任取一张.(1)”抽出红桃”与”抽出黑桃”;(2)”抽出红色牌”与”抽出黑色牌”(3)”抽出牌点数为5的倍数”与”抽出的牌点数大于9”.思路点拨:根据互斥事件与对立事件的定义进行判断.判断是否为互斥事件,主要是看两事件是否同时发生;判断是否为对立事件,首先看是否为互斥事件,然后再看两事件是否必有一个发生,若必有一个发生,则为对立事件,否则,不是对立事件.练习.从装有两个红球和两个黑球的口袋内任取两个球,那么互斥而不对立的两个事件是A.“至少有一个黑球”与“都是黑球”B.“至少有一个黑球”与“至少有一个红球”C.”恰有一个黑球“与“恰有两个黑球”D.“至少有一个黑球”与“都是红球”C例2.某个地区从某年起几年内的新生婴儿数及其中的男婴数如下表(结果保留两位有效数字)时间范围新生婴儿数男婴数男婴出生频率1年内554427162年内901348993年内4年内8590681213520171910.490.540.500.50计算男婴出生频率与概率约是?0.5练习:在某一时期内,一条河流某处的最高水位在各个范围内的概率如下:年最高水位(单位:m)概率0.10.280.380.160.08[8,10)[10,12)[12,14)[14,16)[16,18)计算在同一时期内,河流这一处的年最高水位在下列范围内的概率:(1);(2);(3).[10,16)[8,12)[14,18)例3在一只袋子中装有7个红球,3个绿球,从中无放回地任意抽取两次,每次只取一个,试求:⑴取得两个同颜色球的概率;⑵至少取得一个红球的概率.P=24/45=8/15P=1-3/45=14/151、从1,2,3,4这4个数中,不放回地任意取两个数,两个数都是偶数的概率是()(A)(B)(C)(D)16141312练习2、某人忘记了电话号码的最后一个数字,随意拨号,则拨号不超过三次而接通电话的概率是()103、A109、B81、C101、DAAx>0y>0x+y<33-x-y<1例4取一根长度为3m的绳子,拉直后在任意的两个位置剪断,那么剪得的中间这一段绳子的长度小于1m的概率是多少?yxo33设左右段分别为x,y22xy22211325221932P练习、甲乙两人相约在8点至9点之间在某地碰头,约定早到者到达后应等20分钟方可开.如果两人在8点至9点之间到达的时刻是随机的,求两人相遇的可能性.解:设甲到达时间:x,乙到达时间:y04的概率为()A、4/16B、1/2C、3/16D、5/16甲乙12341234练习222(,),16mnPmnPxy、若以连续两次掷骰子得到的点数、作为的坐标则点在圆内的概率是()365、A367、B92、C31、DCB练习1、向正方形网格随机抛掷半径为1cm的硬币,已知每个小正方形的边长为5cm,求硬币与正方形的边有公共点的概率.练习2.一海豚在水池中自由游弋,水池为长30m、宽20m的长方形,求此海豚离岸边不超过2m的概率.251692525302028184302025