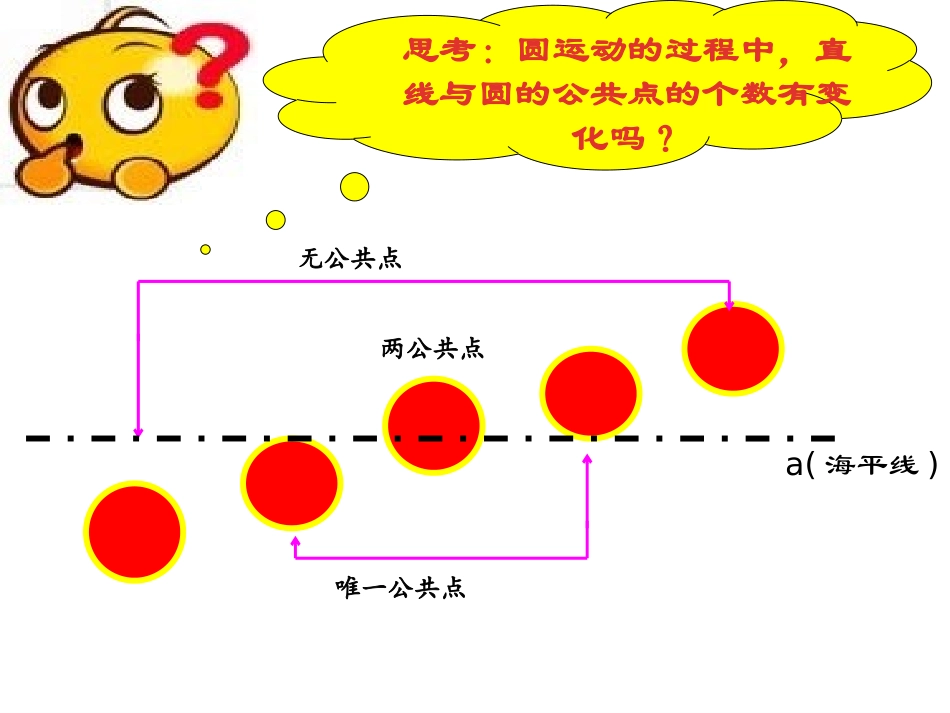
a(海平线)无公共点唯一公共点两公共点思考:圆运动的过程中,直线与圆的公共点的个数有变化吗?特点:叫做直线和圆相交。直线和圆有两个公共点,特点:直线和圆有惟一的公共点,叫做直线和圆相切。这时的直线叫切线惟一的公共点叫切点。特点:直线和圆没有公共点,叫直线和圆相离.A.A.B一:直线与圆的位置关系。(从公共点的个数区分)相切1、看图判断直线L与⊙O的位置关系(1)(2)(3)(4)相离相切相交相交LLL·O·O·O·OL练一练试试看!1.直线与圆最多有两个公共点。…()√×判断3.若A是⊙O上一点,则直线AB与⊙O相切。()2.若直线与圆相交,则直线上的点都在圆内。()4.若C为⊙O外的一点,则过点C的直线CD与⊙O相交或相离。………()××.A.O.C生活中还有哪些例子,能给我们直线与圆的位置关系的印象呢?你能举出几个实例吗?动动手如图,在纸上画一个圆,把直尺的一边看作直线,在纸上移动直尺,在直尺移动的过程中,除了公共点的变化外,还有什么变化吗?.Ord观察讨论:当直线与圆相离、相切、相交时,圆心到直线的距离d与半径r有何关系?dr相切...Odr相离.Oll1、直线与圆相离2、直线与圆相切3、直线与圆相交d>rd=rd5cmd=5cmd<5cm0cm≤210小试牛刀例题:在RtABC△中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?(1)r=2cm;(2)r=2.4cm(3)r=3cm。BCAD453??解:过C作CD⊥AB,垂足为D。在Rt△ABC中,由勾股定理得:AB=5根据三角形面积公式有CD·AB=AC·BC∴CD===2.4即圆心C到AB的距离d=2.4cm2.4例题:Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?(1)r=2cm(2)r=2.4cm(3)r=3cm。ACAD45B3d=2.4d=2.4(1)当r=2cm时,∵d>r,∴⊙C与AB相离。(2)当r=2.4cm时,∵d=r,∴⊙C与AB相切。(3)当r=3cm时,∵d<r,∴⊙C与AB相交。1.如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心、以r为半径的圆与直线OA有怎样的位置关系?为什么?⑴r=2cm;⑵r=4cm;⑶r=2.5cm。OABM解:过点M作MCOA⊥于C,∵∠AOB=30°,OM=5cm,∴MC=2.5cmC⑴∵d=MC=2.5,r=2即d>r∴⊙O与OA相离;⑵∵d=MC=2.5,r=4即d<r∴⊙O与OA相交;⑶∵d=MC=2.5,r=2.5即d=r∴⊙O与OA相切..思考:圆心A到X轴、Y轴的距离各是多少?OXY已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。BC43相离相切A练习同学们:本节课你收获了什么?你还有什么困惑吗???2.识别直线与圆的位置关系的方法:1.直线与圆的三种位置关系:小结(2)性质识别:相离、相切和相交(1)定义识别:直线和圆没有公共点直线和圆有一个公共点直线和圆有两个公共点相离相切相交直线和圆相离直线和圆相切直线和圆相交d>rd=rd