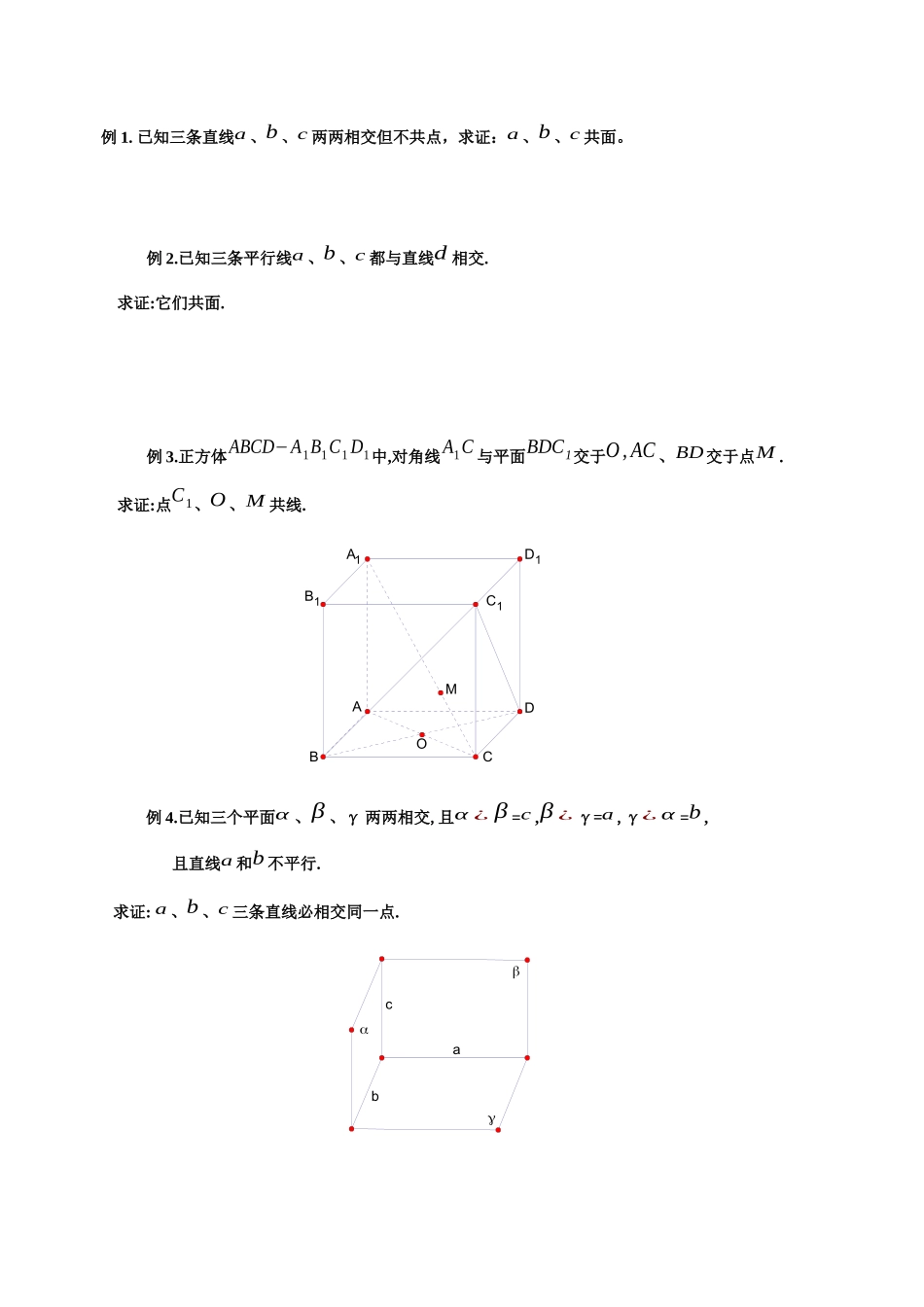
1.2.1平面的基本性质与推论(导学案)1。平面的基本性质:(1)点和直线的基本性质:连接两点的线中,最短;过两点一条直线,并且一条直线。(2)平面的基本性质:10如果一条直线的点在一个平面内,那么这条直线上的所有点在这个平面内。这时我们就说或。作用:20经过同一直线的三点,有且只有个平面。也可以简单地说成:的三点确定一个平面。过不共线的三点A、B、C的平面,通常记作:。作用:30如果不重合的两个平面有个公共点,那么它们有且只有条过这个点的公共直线。如果两个平面有一条公共直线,则称这两个平面。这条公共直线叫做着两个平面的作用:注意:画两个相交平面时,,其中一个平面被另一个平面遮住的部分画成线或。(3)平面的基本性质的推论:10经过一条直线和直线的一点,有且只有个平面。20经过两条直线,有且只有个平面。30经过两条直线,有且只有个平面。三推论作用:(4)共面与异面直线:共面:空间中的几个点或几条直线,如果都在,我们就说它们共面。共面的两条直线的位置关系有和两种。异面直线:既又的直线叫异面直线。判断两条直线为异面直线的方法:与一平面相交于一点的直线与这个平面内的直线是异面直线。(5)符号语言:点A在平面α内,记作;点A不在平面α内,记作。直线l在平面α内,记作;直线l不在平面α内,记作。平面α与平面β相交于直线a,记作.直线l和直线m相交于点A,记作,简记作:。基本性质10可以用集合语言描述为:如果点Aα,点Bα,那么直线ABα。二、典型例题:例1.已知三条直线a、b、c两两相交但不共点,求证:a、b、c共面。例2.已知三条平行线a、b、c都与直线d相交.求证:它们共面.例3.正方体ABCD−A1B1C1D1中,对角线A1C与平面BDC1交于O,AC、BD交于点M.求证:点C1、O、M共线.MOD1C1B1A1DCBA例4.已知三个平面α、β、γ两两相交,且α¿β=c,β¿γ=a,γ¿α=b,且直线a和b不平行.求证:a、b、c三条直线必相交同一点.bac三、学生练习:P38练习A、B补充1。判断题⑴若两个平面有三个不同的公共点,则这两个平面重合.⑵两两相交的三条直线确定一个平面.⑶空间中的三个点确定一个平面.⑷若点A在平面α外,则点A和平面α内的任意一条直线都不共面.2.已知α∩β=l,A∈l,B∉l,B∈α,C∉l,C∈β,则平面ABC¿α=;平面ABC¿β=;平面ABC¿l=.3.根据要求画出图形①直线a在平面α内②直线a在平面α上方③直线a穿过平面α④α∩β=l,a⊂α,a∩γ=P,b⊂β,b∩α=P四、小结:五、作业:1。已知下列四个命题:⑴铺得很平的一张白纸是一个平面;(2)一个平面的面积可以等于6cm2;(3)平面是矩形或平行四边形的形状;(4)两个平面叠在一起比一个平面厚.其中正确的有()个。A0B1C2D32.若点M在直线a上,a在平面α内。则M、a、α间的上述关系可记为()AM∈a,a∈αBM∈a,a⊂αCM⊂a,a⊂αDM⊂a,a∈α3.A、B、C、D四点共面,B、C、D、E四点共面,问A、B、C、D、E五点()A共面B不共面C共线D不确定4.下列哪种情况可确定一个平面()四边形B两两相交且不共点的四条直线C空间三点D三条直线交于一点5。空间有四个点,如果其中任意三个点不共线,则经过其中三个点的平面有()A。2个或3个B。4个或3个C。1个或3个D。1个或4个6。三条直线两两相交,可确定平面的个数为()A。1B。2C。3D。1或37。有以下三个命题:①不在平面内的一条直线与这个平面最多有一个公共点;②直线l在平面α内,可以用符号表示为“l∈α”③若平面α内的一条直线a与平面β内的一条直线b相交,则α与β相交请将所有正确命题的序号写出.8。四条直线最多可确定个平面。9。已知三棱锥S−ABC的侧棱SA、SC与底边AB、BC上各分别有一点P、T、Q、R四点,且PT与QR交于一点K.求证:直线PT、QR、AC共点10。如图,在四面体ABCD中,做截面PQR,若PQ和CB的延长线交于M,RQ和DB的延长线交于N,RP和DC的延长线交于K。求证:M、N、K三点共线.