三角形全等复习课BVIP免费

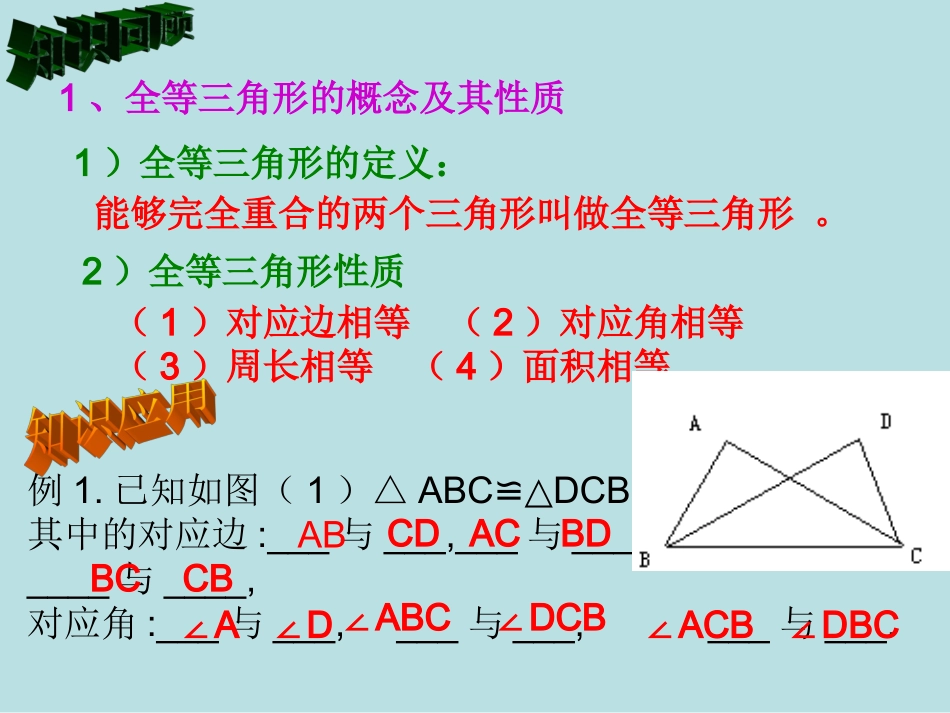
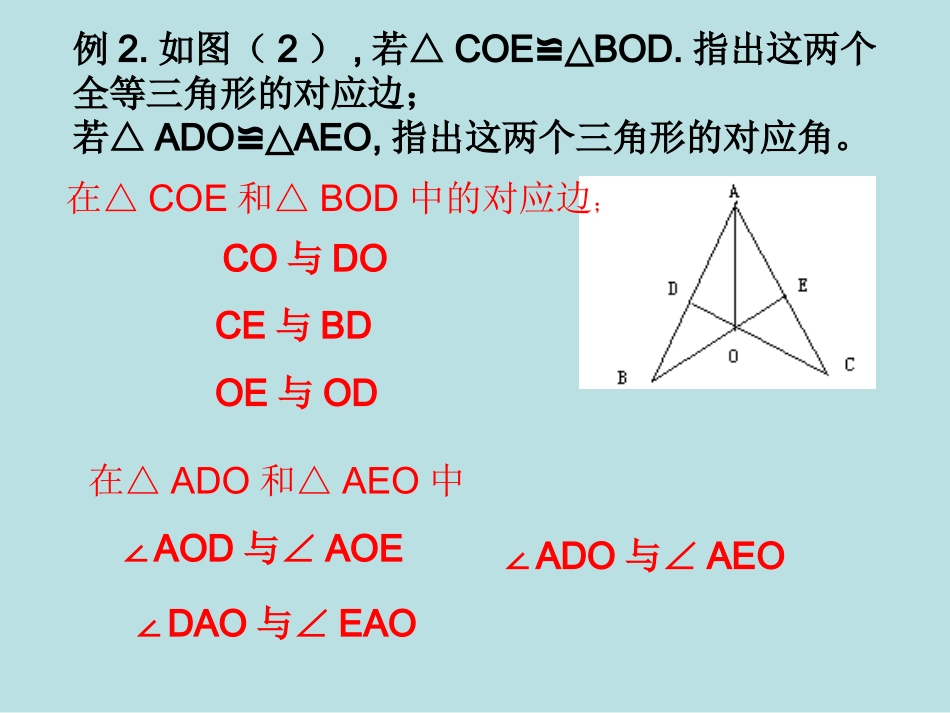
洪湖市双语实验学校王会仁复习课1、全等三角形的概念及其性质1）全等三角形的定义：能够完全重合的两个三角形叫做全等三角形。2）全等三角形性质（1）对应边相等（2）对应角相等（3）周长相等（4）面积相等例1.已知如图（1）△ABCDCB,≌△其中的对应边:___与___,___与___,____与____,对应角:___与___,___与___,___与___.ABCDACBDBCCB∠AD∠∠ABCDCB∠∠ACBDBC∠例2.如图（2）,若△COEBOD.≌△指出这两个全等三角形的对应边；若△ADOAEO,≌△指出这两个三角形的对应角。在△COE和△BOD中的对应边；CO与DOCE与BDOE与OD在△ADO和△AEO中∠AOD与∠AOE∠ADO与∠AEO∠DAO与∠EAO例3．如图（3）,≌，BC的延长线交DA于F，交DE于G,,,求∠EAB、∠DGB的度数.ABCADE105AEDACB解：∵105AEDACB25DB∵10CAD∴∠EAB=1100∵∠CAF+ACF=D+DGB∠∠∠∴∠DGB=25,10DBCAD600500750∴∠BAC=∠DAE=∠ACF=2.全等三角形的判定方法1）、三边对应相等的两个三角形全等(SSS)例1．如图，在中△ABC,，D、E分别为AC、AB上的点，且AD=BD,AE=BC,DE=DC.求证：DEAB⊥。BCADE90C证明：在△BCD和△AED中AE=BCAD=BDDE=DC∴△AEDBCD(SSS)≌△∴∠AED=BCD∠∵∠C=900∴∠AED=900∴DEAB⊥例2.如图，AB=AC,BE和CD相交于P，PB=PC,求证：PD=PE.证明：连接AP在△ABP和△ACP中AP=APAB=ACPB=PC∴∠B=C∠在△BPD和△CPE中∠B=C∠BP=CP∠BPD=CPE∠∴PD=PE.∴∴△ABP≌△ACP△BPD≌△CPE例3.如图，在△ABC中,M在BC上，D在AM上，AB=AC,DB=DC。求证：MB=MC证明：在△ABD和△ACD中AB=ACBD=CDAD=AD∴△ABDACD≌△∴∠BAD=CAD∠在△ABM和△ACM中AB=AC∠BAD=CAD∠AM=AM∴△ABMACM≌△∴BM=CM2）两边和夹角对应相等的两个三角形全等（SAS）例4.如图,AD与BC相交于O,OC=OD,OA=OB,求证：DBACAB在AOC△和△BOD中AO=BO∠AOC=BOD∠CO=DO∴△AOCBOD≌△∴∠C=D,AC=BD∠证明：∵OA=OBOC=OD∴AD=BC在△ABC和△BAD中AD=BC∠D=C∠AC=BD∴△ABCBAD≌△∴∠CAB=DBA∠3）、两角和夹边对应相等的两个三角形全等(ASA)例5.如图，梯形ABCD中，AB//CD，E是BC的中点，直线AE交DC的延长线于F求证：≌ABEFCE证明：∵AB//CD∴∠B=FCE∠∵E是BC的中点∴BE=CE在△ABE和△FCE中∠B=FCE∠BE=CE∠AEB=FCE∠∴△ABEFCE≌△4）、两角和夹边对应相等的两个三角形全等(AAS)证明：∵ABDE∥已知：如图，A、C、F、D在同一直线上，AB＝DE，ABDE∥，BCEF∥，求证：△ABC≌△DEF．BCDEFA∴∠A=D∠∵BCEF∥∴∠BCF=AFE∠∴∠ACB=DFE∠在△ABC和△DEF中∠A=D∠∠BCF=AFE∠AB=DE∴△ABC≌△DEF5）一条直角边和斜边对应相等的两个直角三角形全等(HL)例7.如图，在△ABC中,，沿过点B的一条直线BE折叠，使点C恰好落在AB边的中点D处，则∠A的度数=。90CABC03033．角平分线．角平分线1)。角平分线性质定理：角平分线上的点到这个角两边的距离相等。逆定理：到一个角两边的距离相等的点在这个角的平分线上。例8如图，在△ABC中，，AD平分∠CAB,BC=8cm,BD=5cm，那么D点到直线的距离是．90CACBDE3cm例9.如图,已知在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D.(1)若∠BAC=30°,则AD与BD之间有何数量关系，说明你的理由;(2)若AP平分∠BAC，交BD于P,求∠BPA的度数.PABCDE过D作DEAB⊥于E解:(1)AD=BD∵∠C=,BAC=∠900300∴∠ABC=600∴∠AED=BED=∠900∵BD平分∠ABC∴∠ABD=CBD=∠300∴∠ABD=BAC∠在和△ADEBDE△中∠AED=BED∠∠ABD=BAC∠DE=DE∴△ADEBDE≌△∴AD=BD(2)AP∵平分∠BAD∠BAC=∴∠BAP=150300∵∠ABD=300∴∠BPA=13501、全等三角形的性质2、全等三角形的判定3、全等三角形有关知识的应用课本复习题11