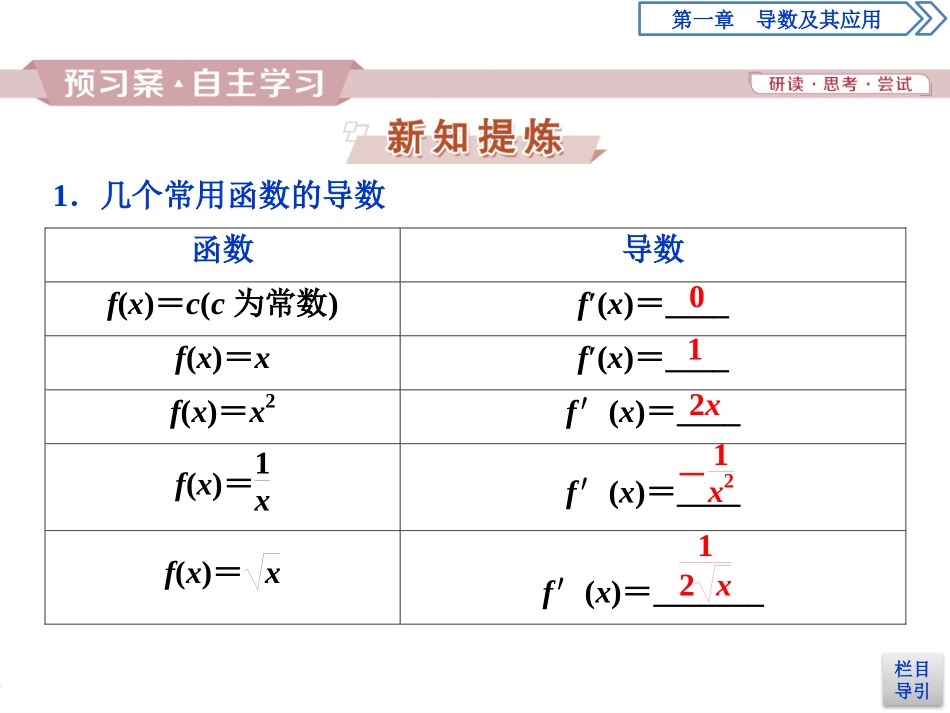
栏目导引应用案巩固提升第一章导数及其应用1.2.1几个常用函数的导数应用案巩固提升1.能根据定义求函数y=c(c为常数),y=x,y=x2,y=1x,y=x的导数.2.能利用给出的基本初等函数的导数公式求简单函数的导数.栏目导引应用案巩固提升第一章导数及其应用1.几个常用函数的导数函数导数f(x)=c(c为常数)f′(x)=____f(x)=xf′(x)=____f(x)=x2f′(x)=____f(x)=1xf′(x)=____f(x)=xf′(x)=_______012x-1x212x栏目导引应用案巩固提升第一章导数及其应用2.基本初等函数的导数公式函数导数f(x)=c(c为常数)f′(x)=______f(x)=xα(α∈Q*)f′(x)=______f(x)=sinxf′(x)=______f(x)=cosxf′(x)=______f(x)=axf′(x)=______f(x)=exf′(x)=______f(x)=logaxf′(x)=______f(x)=lnxf′(x)=______0αxα-1cosx-sinxaxlnaex1xlna1x栏目导引应用案巩固提升第一章导数及其应用(1)上述导数公式表是比较全面的,涵盖了基本初等函数中的常数函数、指数函数、对数函数、幂函数和三角函数,其中幂函数的导数公式中幂指数可以推广到全体实数.(2)若函数式中含有根式,一般将其转化为分数指数幂的形式,再利用y=xα的导数公式解决.(3)记忆正弦函数、余弦函数的导数时,一要注意函数名的变化,二要注意符号的变化.(4)指数函数的导数等于指数函数本身乘以底数的自然对数.(5)对数函数的导数等于x与底数的自然对数乘积的倒数.栏目导引应用案巩固提升第一章导数及其应用判断正误(正确的打“√”,错误的打“×”)(1)sinπ3′=cosπ3.()(2)因为(lnx)′=1x,所以1x′=lnx.()(3)若f′(x)=sinx,则f(x)=cosx.()答案:(1)×(2)×(3)×栏目导引应用案巩固提升第一章导数及其应用已知f(x)=x,则f′(4)=()A.-14B.14C.-2D.2解析:选B.因为f′(x)=12x,所以f′(4)=124=14.曲线y=sinx在x=0处的切线的倾斜角是()A.π2B.π3C.π6D.π4解析:选D.由题知,y′=cosx,所以y′|x=0=cos0=1.设此切线的倾斜角为α,则tanα=1,因为α∈[0,π),所以α=π4.栏目导引应用案巩固提升第一章导数及其应用已知f(x)=2x,则f′1ln2=________.解析:因为f(x)=2x,所以f′(x)=2xln2,所以f′1ln2=f′(log2e)=2log2eln2=eln2.答案:eln2栏目导引应用案巩固提升第一章导数及其应用探究点1运用导数公式求导数求下列函数的导数.(1)y=2018;(2)y=13x2;(3)y=3x;(4)y=log3x.【解】(1)因为y=2018,所以y′=(2018)′=0.栏目导引应用案巩固提升第一章导数及其应用(2)因为y=13x2=x-23,所以y′=-23x-23-1=-23x-53.(3)因为y=3x,所以y′=3xln3.(4)因为y=log3x,所以y′=1xln3.栏目导引应用案巩固提升第一章导数及其应用用公式求函数导数的方法(1)若所求函数符合导数公式,则直接利用公式求解.(2)对于不能直接利用公式的类型,关键是合理转化函数的关系式为可以直接应用公式的基本函数的模式,如y=1x4可以写成y=x-4,y=5x3可以写成y=x35等,这样就可以直接使用幂函数的求导公式求导,以免在求导过程中出现指数或系数的运算失误.栏目导引应用案巩固提升第一章导数及其应用1.已知函数f(x)=x3,x<0lnx,0