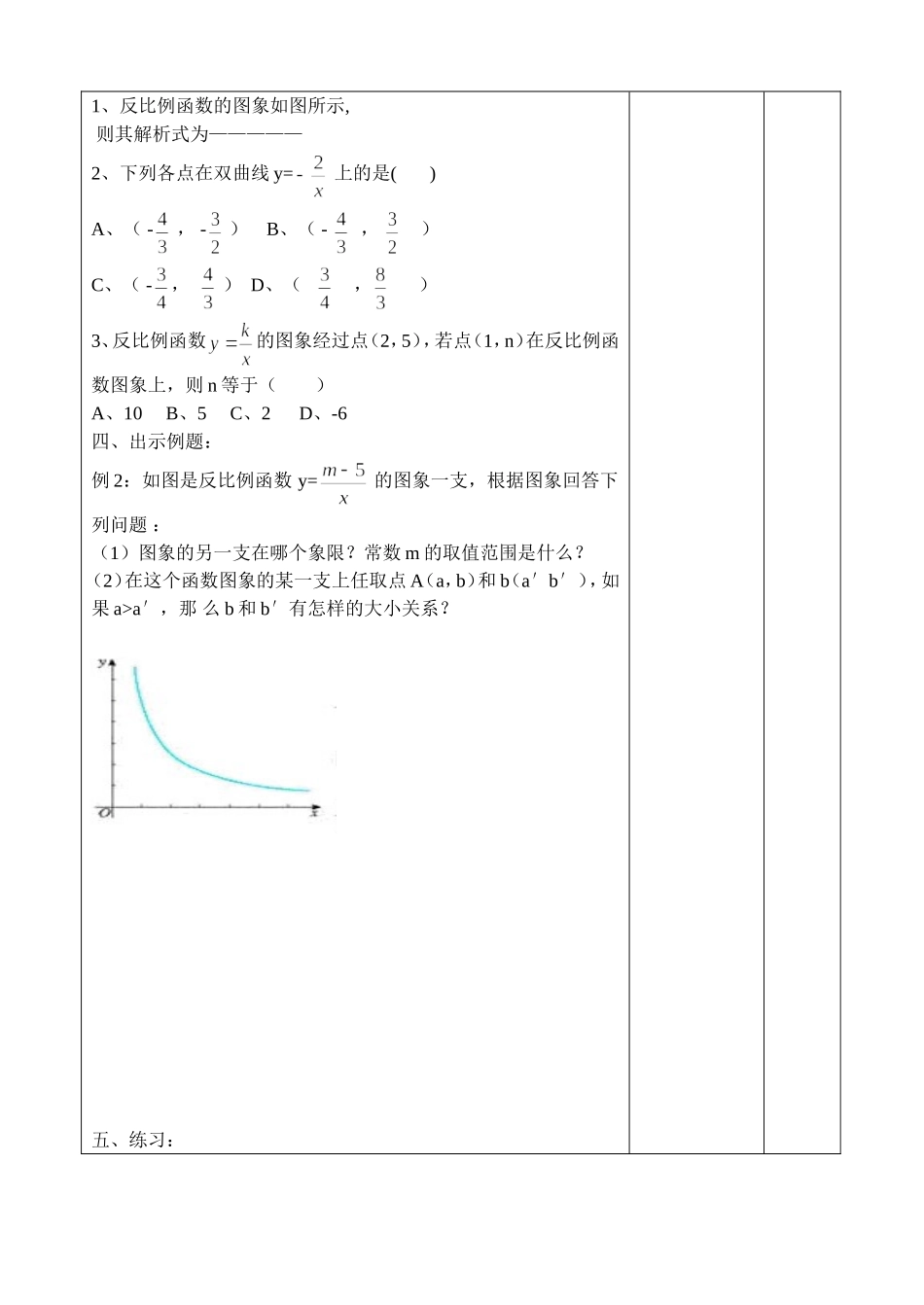
学习指导案年月日课题反比例图像和性质(2)课型新授课课时50学习目标会用待定系数法求反比例函数解析式,运用反比例函数性质解决相关问题学习重点用待定系数法求反比例函数解析式学习难点运用反比例函数性质解决相关问题学习过程学习方式及学习内容.学生领悟(知识、方法)时间一、课前展示反比例图像和性质:::二、引课新授例1:已知反比例函数的图象经过点A(2,6).(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?(2)点B(3,4)、C(-2.5,-4.8)和D(2,5)是否在这个函数的图象上?′学习过程学习方式及学习内容.学生领悟(知识、方法)时间三、巩固练习:yxo2-1A1、反比例函数的图象如图所示,则其解析式为—————2、下列各点在双曲线y=上的是()A、(-,-)B、(-,)C、(-,)D、(,)3、反比例函数的图象经过点(2,5),若点(1,n)在反比例函数图象上,则n等于()A、10B、5C、2D、-6四、出示例题:例2:如图是反比例函数y=的图象一支,根据图象回答下列问题:(1)图象的另一支在哪个象限?常数m的取值范围是什么?(2)在这个函数图象的某一支上任取点A(a,b)和b(a′b′),如果a>a′,那么b和b′有怎样的大小关系?五、练习:1.已知点A(-2,y1),B(-1,y2)都在反比例函数的图象上,则y1与y2的大小关系为——————2已知点A(X,Y)B(X,Y)C(X,Y)且X<0x2>0>x3,则下列各式中正确的是()A、y3>y1>y2B、y3>y2>y1C、y1>y2>y3D、y1>y3>y2六、能力拓展:1.如图,点P是反比例函数y=图象上的一点,PD⊥x轴于D.则△POD的面积为____________2.,点P是反比例函数y=图象上的一点,PA⊥x轴于A,PB⊥y轴于B.则长方形PAOB的面积为___________________3、如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是————————点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是——————4一个反比例函数在第三象限,若A是图象上任意一点,AM⊥y轴于M,O是原点,如果△AOM的面积是3,那么这个反比例函数的解析式是什么?5、如图A、C是反比例函数上任意两点,过A作x轴垂线,垂足为B,过C作y轴垂线,垂足为D,分别与原点构成直角三角形面积为S和S,则S和S数量关系为————————6.若ab<0,则函数y=ax与y=在同一平面直角坐标系中的图象大致是PDoyxPDoyxABoyxCDS1S27.如图,已知反比例函数y=的图象与一次函数y=kx+4的图象相交于P、Q两点,且P点的纵坐标是6。(1)求这个一次函数的解析式(2)求三角形POQ的面积课后作业:作业题目ABC作业超市套餐:A、○○B、○○○C、○○○☆备课辅助案年月日课题课型课时xyoPQDC教材分析学情分析板书设计当堂检测检测结果分析:(检测内容可附在后面)课后反思