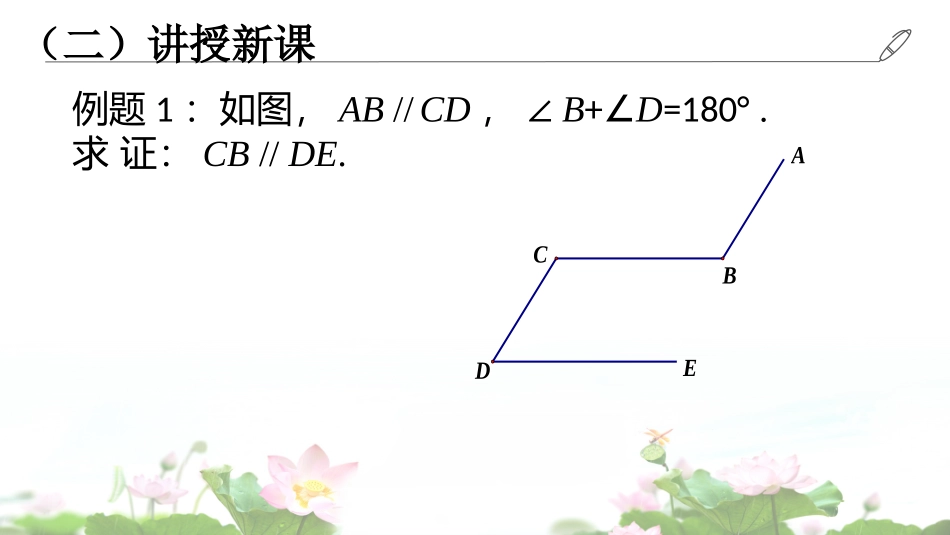
管红娟§19.2证明举例(1)看图填空:(1)因为∠1=2∠(已知)所以∥()(2)因为∠3=75°,∠4=75°(已知)所以=()所以∥()(3)因为∠C=60°,∠ABC=120°(已知)所以=()所以∥()(4)因为AD∥BC(已知)所以____________________________________________________(写出3个结论)(一)知识回顾4321EDCBA同位角相等,两直线平行内错角相等,两直线平行∠1=2∠∠A+∠ABC=180°∠ADB=∠DBCADBC∠3∠4ABDC∠C+ABC∠180°ABDC等量代换等式性质同旁内角互补,两直线平行(二)讲授新课例题1:如图,AB//CD,∠B+∠D=180°.求证:CB//DE.EDCBA变式练习1已知:如图,四边形ABCD中,AB//CD,∠B=∠D.求证:AD//BC.DCBA例题2:如图,点D、E、F分别是AC、AB、BC上的一点,DF//AB,∠DFE=∠A.求证:EF//AC.变式练习2(课后思考):从已知条件DF∥AB和∠DFE=∠A中任选一个作为结论,将求证EF∥AC作为条件,再证明.(三)巩固练习练习1:如图,AC与BD相交于点O,∠A=∠AOB,∠C=∠COD.求证:AB//CD.ODCBA练习2:如图,点D、E分别在△ABC的边AB、AC边上,AB=AC.(1)如果DE//BC,求证:AD=AE.(2)如果AD=AE,求证:DE//BC.练习2:已知:如图,点D、E分别在的边AB、AC上,AB=AC.(1)如果DE//BC,求证:AD=AE.21EDCBA??分析:要证明AD=AE,只要证明________,由已知条件DE//BC可得:________,________,只需证明________,由已知条件AB=AC可得.∠1=∠2∠1=∠B∠2=∠C∠B=∠C试着分析本题的解题方法.练习2:如图,点D、E分别在的边AB、AC上,AB=AC.(1)如果DE//BC,求证:AD=AE.21EDCBA??证明:∵DE//BC(已知),∴∠1=∠B().两直线平行,同位角相等同理:∠2=∠C.又∵AB=AC(已知),∴∠B=∠C().等边对等角∴∠1=2∠(等量代换).∴AD=AE().等角对等边练习2:如图,点D、E分别在的边AB、AC上,AB=AC.(2)如果AD=AE,求证:DE//BC.21EDCBA23证明题的分析思路证明两条直线平行的方法1(四)小结:分析过程:要证什么需证什么已知什么证明过程:已知结论可知分析过程:要证什么需证什么已知什么证明过程:已知结论可知主要利用平行线的判定和性质证明题书写格式的规范拓展延伸已知:如图,在四边形ABCD中,AB=CD,∠B=∠C,BE=CF.求证:AD//BC.GFEDCBA分层作业巩固基础:练习册习题19.2(1)、变式练习2(五)作业布置水陆草木之花,可爱者甚蕃。晋陶渊明独爱菊。自李唐来,世人盛爱牡丹。予独爱莲之出淤泥而不染,濯清涟而不妖,中通外直,不蔓不枝,香远益清,亭亭净植,可远观而不可亵玩焉。予谓菊,花之隐逸者也;牡丹,花之富贵者也;莲,花之君子者也。噫!菊之爱,陶后鲜有闻。莲之爱,同予者何人?牡丹之爱,宜乎众矣!感谢各位专家老师的聆听!莲说