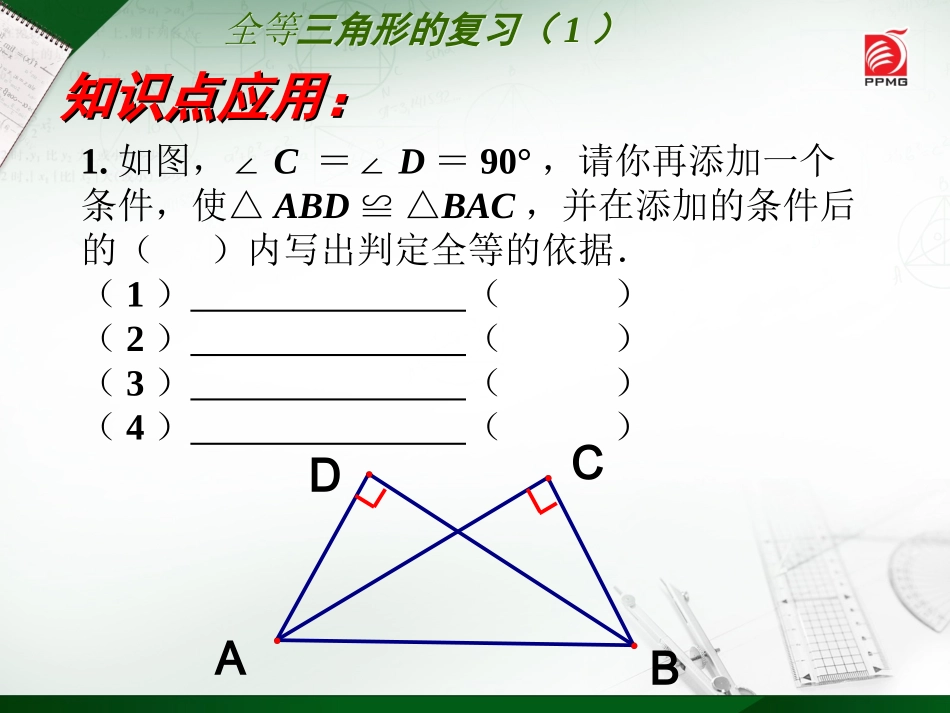
八年级(上册)初中数学扬中市第一中学2013-10-31第一章全等三角形(复习课)一、知识梳理全等图形全等三角形特殊情况特殊情况定义:定义:能够完全重合的图形性质:性质:形状大小都相等对应边、对应角相等性质:性质:判定:判定:SASSASASAASAAASAASSSSSSS一般三角形一般三角形直角三角形直角三角形HLHLCBAD1.如图,∠C=∠D=90°,请你再添加一个条件,使△ABD≌△BAC,并在添加的条件后的()内写出判定全等的依据.(1)()(2)()(3)()(4)()全等三角形的复习(1)全等三角形的复习(1)知识点应用:知识点应用:2.如图所示,已知等边△ABC中,BD=CE,AD与BE相交于点P,(1)求证:△ABD≌△BCE(2)APE∠是度.全等三角形的复习(1)全等三角形的复习(1)3.如图所示,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,(1)求证:BD=AE;(2)BGCAFC△≌△吗?△DCGECF≌△吗?(3)求锐角∠DOE的度数。O全等三角形的复习(1)全等三角形的复习(1)变式一、如图,△ABC和△CDE均为等边三角形,BD,AE交于点O)1(求证:BD=AE;)2(求锐角∠BOA的度数。ECBADO●全等三角形的复习(1)全等三角形的复习(1)4.如图,AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:CF=DF.提示:连接AC、AD.EDFCBADABECF全等三角形的复习(1)全等三角形的复习(1)变式一、如图,AB=AE,BC=ED,∠B=∠E,CF=DF,F为垂足,求证:AF⊥CD.提示:连接AC、AD.EDFCBADABECF5.如图所示,已知AEAB⊥,AFAC⊥,AE=AB,AF=AC.求证:(1)EC=BF;(2)ECBF.⊥全等三角形的复习(1)全等三角形的复习(1)31247568∟∟EBA∟F∟C变式一、如图,在△COD中,CO=DO,CODO,⊥在△AOB中,AO=BO,AOBO⊥试猜想CE与BF的关系,并说明理由D4675全等三角形的复习(1)全等三角形的复习(1)1326(1)如图(1),已知:△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.213变式一、(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=AEC=BAC=α∠∠,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.2131.如图1,△ABCAEF,ABC=30°,≌△∠BAE=x,AE∠和BC交于点D(1)△ABE是三角形;(2)用x表示△BDE的三个内角;)3(当△BDE有两个角相等时,求x的值.全等三角形的复习(1)全等三角形的复习(1)拓展与延伸拓展与延伸::ABCDEMN1231.如图,∠1=∠2=∠3,AB=AD,AC=AE求证:(1)ABCADE△≌△;(2)AM=AN检测与反馈检测与反馈::∟∟ABCDEFG2.已知:如图,BD、CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,GC=AB,试猜想CE与BF的关系,并说明理由.13245