3.1双曲线及其标准方程VIP免费

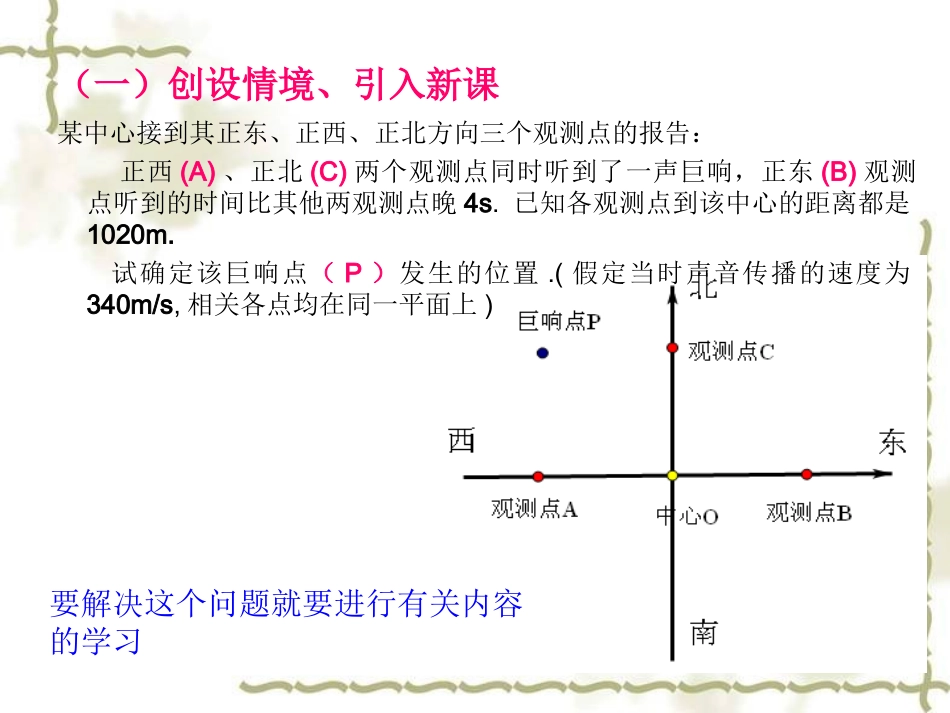
§3.3-1双曲线及其标准方程崇仁二中李建明某中心接到其正东、正西、正北方向三个观测点的报告：正西(A)、正北(C)两个观测点同时听到了一声巨响，正东(B)观测点听到的时间比其他两观测点晚4s.已知各观测点到该中心的距离都是1020m.试确定该巨响点（P）发生的位置.(假定当时声音传播的速度为340m/s,相关各点均在同一平面上)（一）创设情境、引入新课要解决这个问题就要进行有关内容的学习(二)诱导尝试、探究新知探究一：双曲线的定义演示一探究二：双曲线的标准方程演示二探究二：双曲线的标准方程1.建系:以F1,F2所在的直线为x轴，线段F1F2的中点为原点建立直角坐标系2.设点:设M（x,y）,则F1(-c,0),F2(c,0)3.列式:|MF1|-|MF2|=±2aaycxycx2)()(2222即||MF1|-|MF2||=2a4.化简:aycxycx2)()(2222222222)(2)(ycxaycx222()cxaaxcy)()(22222222acayaxac此即为焦点在x轴上的双曲线的标准方程22221(0,0)xyabab所以得：222cab令思考2：121221(c,0)(c,0)2a2a已知两定点1）若动点满足则动点的轨迹是什么,并写出其轨迹方程2）若动点满足则动点的轨迹是什么,并写出其轨迹，，方程FFPPFPFPPPFPFP1）2）点P的轨迹是双曲线的右支点P的轨迹是双曲线的左支2222:(01)xyabx轨迹方程2222:(01)xyabx轨迹方程若建系时,焦点在y轴上标准方程？22221xyab22221yxab焦点位置：前的系数，哪一个为正，则焦点在哪一个轴上22,yx222c(00)abab，若双曲线上有一点Ｐ，且|ＰF1|=10,则|ＰF2|=_________例1已知双曲线的焦点为F1(-5,0),F2(5,0)，双曲线上一点P到F1、F2的距离的差的绝对值等于6，求双曲线的标准方程.∵∵22aa=6,=6,c=5c=5∴∴aa=3,c==3,c=55∴∴bb22=5=522--3322=16=16所以所求双曲线的标准方程为：所以所求双曲线的标准方程为：116922yx根据双曲线的焦点在根据双曲线的焦点在xx轴上，设它的标准方程为轴上，设它的标准方程为：：)0,0(12222babyax解:4或16（三）知识巩固、强化提高22.:121xymmm如果方程表示双曲线，求变的取值范围式解:2<01<0mm2m得∴m的取值范围为(,2)解:(2)(1)0mm由21mm得或∴m的取值范围为(,2)(1,)22121xymm例2：方程表示焦点在y轴的双曲线时，则m的取值范围.某中心接到其正东、正西、正北方向三个观测点的报告：正西(A)、正北(C)两个观测点同时听到了一声巨响，正东(B)观测点听到的时间比其他两观测点晚4s.已知各观测点到该中心的距离都是1020m.试确定该巨响点（P）发生的位置.(假定当时声音传播的速度为340m/s,相关各点均在同一平面上)分析：1)|PA|=|PC|2)|PB|－|PA|=340×4=1360问题解决故:1)P在AC的垂直平分线上2)由双曲线定义知P点在以A、B为焦点的双曲线的一支上只要能把巨响点P满足的两个曲线方程求出来.那么解方程组就可以确定巨响点的位置.解：如图，以接报中心为原点O，正东、正北方向为x轴、y轴正向，建立直角坐标系.设A、B、C分别是西、东、北观测点，则A(－1020,0），B(1020,0），C(0,1020）.设P（x,y）为巨响点，由A、C同时听到巨响声，得|PA|=|PC|,故P在AC的垂直平分线PO上,PO的方程为y=－x，因B点比A点晚4s听到爆炸声，故|PB|－|PA|=340×4=1360,由双曲线定义知P点在以A、B为焦点的双曲线22221xyab的一支上，依题意得a=680,c=1020，22222210206805340bca∴双曲线的方程为222216805340xy用y=－x代入上式，得5680x，∵|PB|>|PA|,6805,6805,(6805,6805),68010xyPPO即故答:巨响发生在接报中心的西偏北450距中心68010m处.（四）课堂小结、知识提炼1．双曲线的定义；2．双曲线的标准方程（五）课后作业、理解运用1.课本第一题80p2.新课程新练习