高三数学翰林高考2010猜射测试卷文科(必修+选修I)卷(四)VIP免费

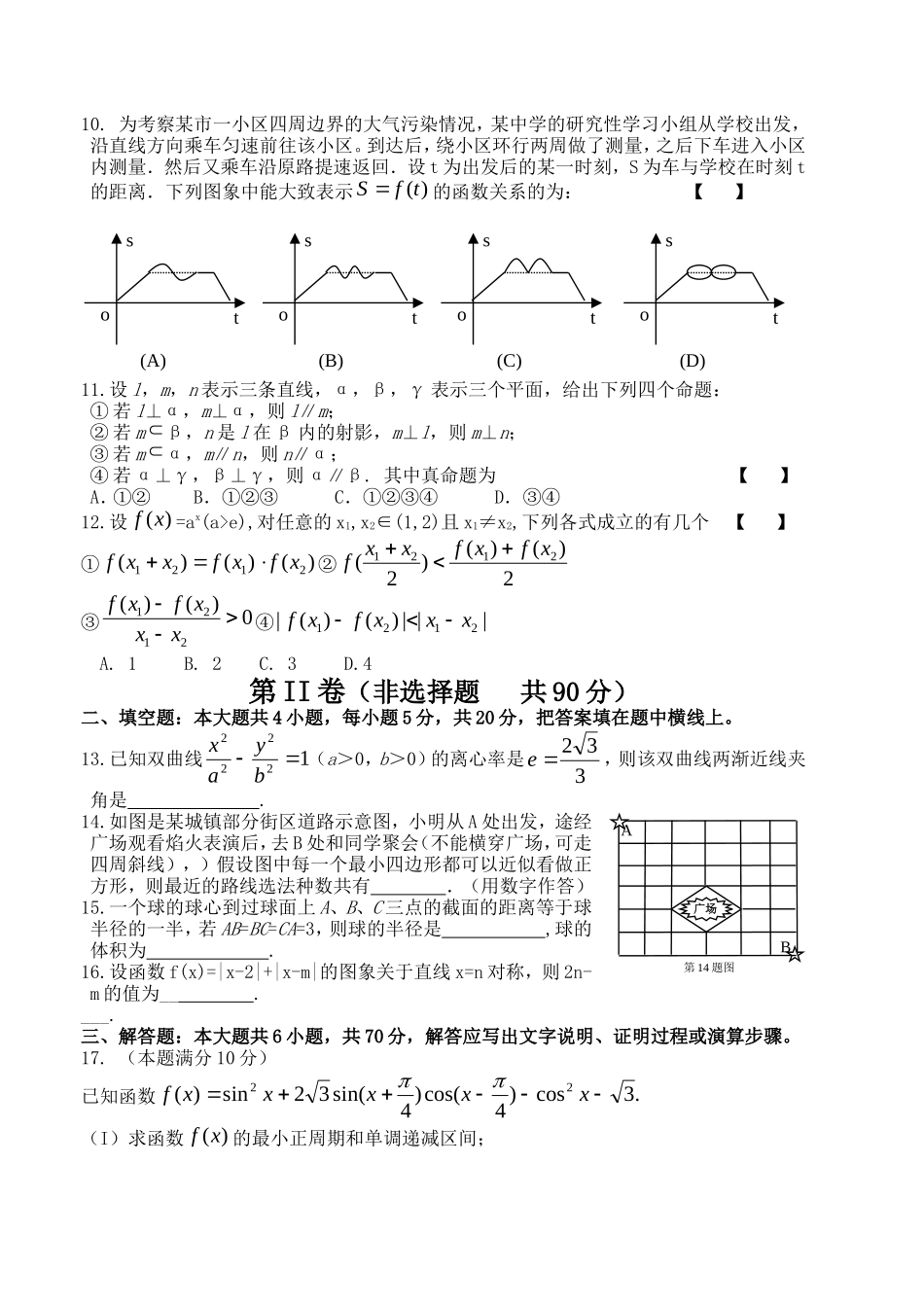
翰林高考2010猜射数学文科（必修+选修I）卷（四）学校___________班级________考号__________姓名__________第Ⅰ卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合题目要求的。1.如图，U是全集，M、P、S是U的3个子集，则阴影部分所表示的集合是【】A．SPM)(B．SPM)(C．SCPMU)(D．SCPMU)(2.“a+c>b+d”是“a>b且c>d”的【】A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分也不必要条件3.在ABC中,角A、B、C所对的边分别为30,3,,,Baccba如果,那么角C等于A．120°B．105°C．90°D．75°【】4.使函数y=sinx递减且函数y=cosx递增的区间是【】A．2,23B．)(22,2ZkkkC．)(2,22ZkkkD．)(2,22Zkkk5.已知正三棱锥PABC-的底面边长为１，D为PA的中点，若异面直线BD与PC所成的角为q，且3cos6q=，则该正三棱锥的侧棱长是【】Ａ．４Ｂ．３Ｃ．２Ｄ．１6.设),(a为221)(xxxf反函数的一个单调递增区间,则实数a的取值范围为A.2aB.2aC.2aD.2a【】7.123)1(xx展开式中的常数项为【】A.－1320B.1320C.－220D.2208.若0x，0y，且1yx，那么24yx的最小值为【】A.4B.25C.1D.09.等差数列{an}的前n项和为Sn，若a2+a6+a13为一个确定的常数，则下列各个和中，也为确定的常数的是【】A．S6B．S13C．S12D．S1110.为考察某市一小区四周边界的大气污染情况，某中学的研究性学习小组从学校出发，沿直线方向乘车匀速前往该小区。到达后，绕小区环行两周做了测量，之后下车进入小区内测量．然后又乘车沿原路提速返回．设t为出发后的某一时刻，S为车与学校在时刻t的距离．下列图象中能大致表示()Sft的函数关系的为：【】11.设l，m，n表示三条直线，α，β，γ表示三个平面，给出下列四个命题：①若l⊥α，m⊥α，则l∥m；②若mβ，n是l在β内的射影，m⊥l，则m⊥n；③若mα，m∥n，则n∥α；④若α⊥γ，β⊥γ，则α∥β.其中真命题为【】A．①②B．①②③C．①②③④D．③④.w.w.k.s.5.u.c.o.m12.设)(xf=ax(a>e),对任意的x1,x2∈(1,2)且x1≠x2,下列各式成立的有几个【】①)()()(2121xfxfxxf②2)()()2(2121xfxfxxf③0)()(2121xxxfxf④|||)()(|2121xxxfxfA.1B.2C.3D.4第II卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上。13.已知双曲线12222byax（a＞0，b＞0）的离心率是332e，则该双曲线两渐近线夹角是.14.如图是某城镇部分街区道路示意图，小明从A处出发，途经广场观看焰火表演后，去B处和同学聚会（不能横穿广场，可走四周斜线），）假设图中每一个最小四边形都可以近似看做正方形，则最近的路线选法种数共有．（用数字作答）15.一个球的球心到过球面上A、B、C三点的截面的距离等于球半径的一半，若AB=BC=CA=3，则球的半径是,球的体积为.16.设函数f(x)=|x-2|+|x-m|的图象关于直线x=n对称，则2n-m的值为__.___.三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤。17.（本题满分10分）已知函数.3cos)4cos()4sin(32sin)(22xxxxxf（I）求函数)(xf的最小正周期和单调递减区间；BA广场第14题图tso(A)tso(B)tso(C)tso(D)（II）求函数)(xf在]3625,12[上的最大值和最小值并指出此时相应的x的值.18（本题满分12分）如图，正四棱柱1111DCBAABCD中，E在棱1CC上且CEEC31，CA1平面BED.（I）证明：AA1=2AB；（II）求二面角A1-BD-E的余弦值.19.（本题满分12分）志愿者上岗前需经过服务常识测试.试题由8道选择题组成,每个选择题都给了4个选项(其中有且仅有一个选项是正确的).评分标准规定:每题只选1项,答对得5分,不答或答错得0分.某考生每道题都给出了答案,已确定有4道题的答案是正确的,而其余的题中,有两道题每题都可判断其有两个选项是错误的,有一道题可以判断其一个选项是错误的,还有一道题因未理解题意只好随意填涂.对于该测试者,试求:(Ⅰ)得分为40分的概率;(...