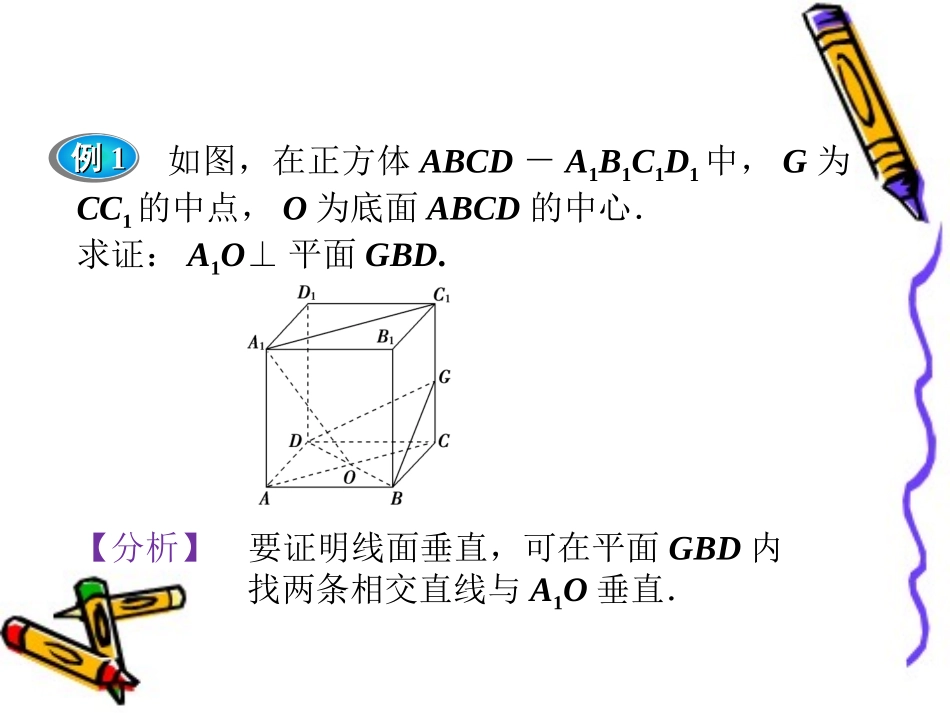
拓展训练线面垂直的判定关键证明线垂直于平面内的两条相交直线.如图,在正方体ABCD-A1B1C1D1中,G为CC1的中点,O为底面ABCD的中心.求证:A1O⊥平面GBD.【分析】要证明线面垂直,可在平面GBD内找两条相交直线与A1O垂直.例例11【证明】∵A1A⊥BDAC⊥BDA1A∩AC=A⇒BD⊥平面A1AOA1O⊂平面A1AO⇒BD⊥A1O,设正方体棱长为a,连接OG、A1G、A1C1.∵A1O2=A1A2+AO2=a2+(22a)2=32a2,OG2=OC2+CG2=(22a)2+(a2)2=34a2,A1G2=A1C21+C1G2=(2a)2+(a2)2=94a2,∴A1O2+OG2=A1G2,∴A1O⊥OG,又∵BD∩OG=O,∴A1O⊥平面GBD.【点评】把线面垂直的证明,转化为线线垂直,其中勾股定理是证明线线垂直的重要方法.跟踪训练1正方体A1B1C1D1-ABCD中,E、F分别是棱AB、BC的中点,O是下底面ABCD的中心,求证:EF⊥平面BB1O.证明:如图所示,连接AC,BD,则O为AC和BD的交点.∵ABCD是正方形,∴AC⊥BO.又∵B1B⊥面ABCD,AC⊂面ABCD,∴BB1⊥AC.又BO∩BB1=B,∴AC⊥面BB1O.又∵E、F分别是AB、BC的中点,∴在△ABC中,EF∥AC.∴EF⊥平面BB1O.