2.4.1向量的数量积-(2)VIP免费

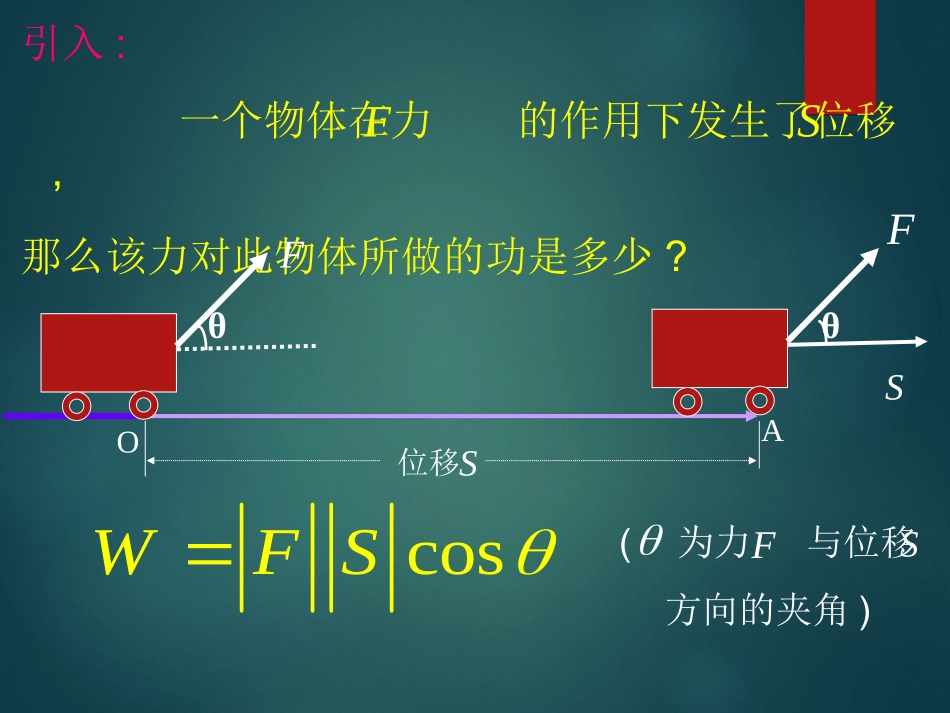
向量的数量积无锡市第六高级中学李凌引入:一个物体在力的作用下发生了位移,那么该力对此物体所做的功是多少?F�S�S�θS�F�θF�位移OAcosWFS�(为力与位移方向的夹角)F�S�cosabOABabF�S�(为向量与的夹角)ab向量的夹角对于两个非零向量和,作,,则叫做向量与向量的夹角abOAa�OBb�AOBabbaOABab范围:0,向量的数量积已知两个非零向量和,它们的夹角是,我们把数量叫做向量和的数量积,记作,即abbcosabaababcosab规定:零向量与任一向量的数量积为0当时,0当时,当时,2与同向;abOABab此时,abab与反向;abOABab此时,abab与垂直,ababOABab记作,0ab此时例1.已知向量与向量的夹角为,,,分别在下列条件下求.abab2a�3b�(1)135(2)//ab(3)ab解(1):2cos13523()322abab��解(2):当时,或.//ab0180若,.1806abab6abab0若abcosab(0,0)ab思考1:当时,反之成立吗?ab0ab思考2:若,则ab?aa思考3:若已知以及的大小,如何求出向量与的夹角?,ab��abab数量积的运算律(1)abba(2)()abcacbc(3)()()()()abababR例2:已知,,向量与的夹角是,求:5a4bab120解:2(1)()()(2)()ababab22()()ababaabbab22ab251692(2)()ab解:2()()()ababab22aabbab222aabb25201621变式1:已知,,向量与的夹角是,求.5a4bab120ab��变式2:已知,,,求向量与的夹角.5a4b61ab�ab变式3:已知,求.abab��ab变式4:已知,,向量与的夹角是,求使与垂直的的值.5a4bab120abab例3.用向量数量积的运算证明:平行四边形四边的平方和等于两条对角线的平方和.