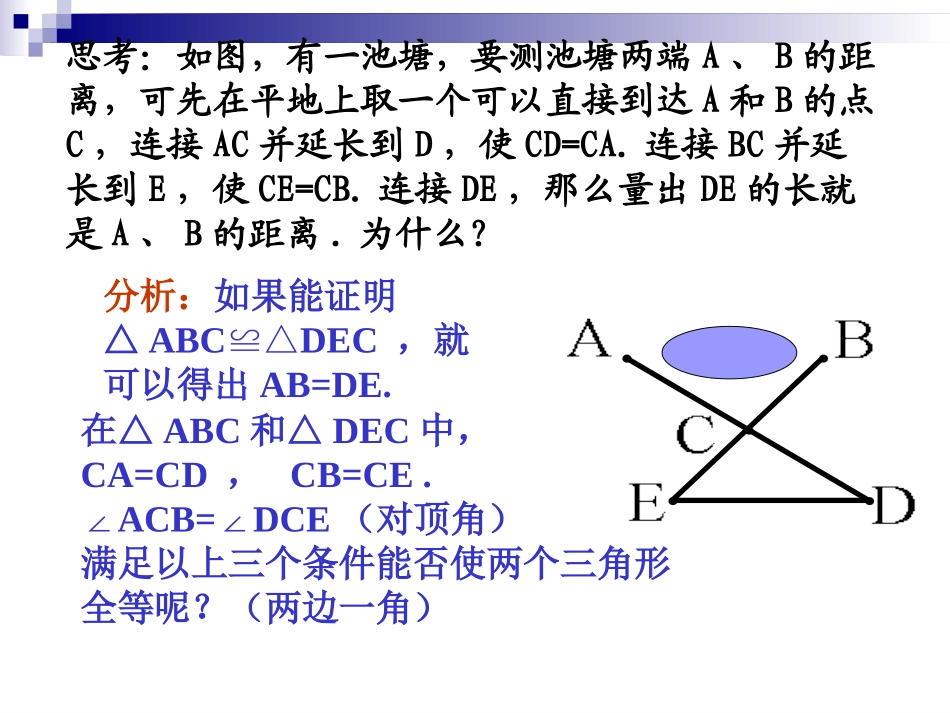
12.2三角形全等的判定SAS1、边边边公理(三边对应相等的两个三角形全等)2、转化思想证线段位置关系(垂直、平行)角平分线求角度数、数量关系角相等证三角形全等找三条对应相等的边找对应相等的边:公共边、中点或中线、通过计算(同加或同减)、做辅助线(构造公共边等)思考:如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?分析:如果能证明△ABCDEC≌△,就可以得出AB=DE.在△ABC和△DEC中,CA=CD,CB=CE.∠ACB=DCE∠(对顶角)满足以上三个条件能否使两个三角形全等呢?(两边一角)9画△ABC,使AB=3cm,AC=4cm。画法:2.在射线AM上截取AB=3cm3.在射线AN上截取AC=4cm若再加一个条件,使∠A=45°,画出△ABC1.画∠MAN=45°4.连接BC则△ABC就是所求的三角形把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?探究新知1由前边的作图比较过程,我们可以得出什么结论?用符号语言表达为:在△ABC与△DEF中AB=DE∠A=D∠AC=DF∴△ABCDEF≌△(SAS)注意“角”放在中间ABCDEF两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或““SASSAS””探究新知2⑵边-边-角(角不夹在两边的中间,形成两边一对角)做一做已知两条线段和一个角,以长的线段为已知角的邻边,短的线段为已知角的对边,画一个三角形.3cm4cm45°步骤:1、画一线段AB,使它等于4cm;2、画∠BAM=45°;3、以B为圆心,3cm长为半径画弧,交AM于点C;4、连结CB.△ABC即为所求.把你画的三角形与其他同学画的三角形进行比较,所有的三角形都全等吗?探究新知⑵ABMCD结论:两边及其一边所对的角相等,两个三角形不一定全等.ABCABD例题1、如图,B点在A点的正北方向。两车从路段AB的一端A出发,分别向东、向西进行相同的距离,到达C、D两地。此时C,D到B的距离相等吗?为什么?BDAC【证明】依题意的AB⊥DC,AD=ACBA=BA∠BAD=BAC∠AD=AC则△BAD≌△BAC(SAS).即BD=BC寻找对应相等的边角边公共边-对应边垂直-对应角(90°)中点-对应边 AB⊥DCBAD=BAC=90°∴∠∠在△BAD和△BAC中,例题⑵已知:如图,直线AC和直线BD相交于点O,OA=OC,OB=OD,求证:AB=CD。OACBD知识应用例3.如图,有一池塘,要测池塘端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长到D,使CD=CA.连结BC并延长到E,使CE=CB.连结DE,那么量出DE的长,就是A、B的距离.为什么?ABCED巩固练习1、如图,点E、F在BC上,BE=CF,AB=DC,∠B=C∠,求证:∠A=D∠ADBEFC【证明】 BF=BE+EFCE=CF+FE而BE=CF∴BF=CE在△ABF和△DCE中,BF=CE∠B=C∠AB=DC∴△ABF≌△DCE(SAS)即∠A=D∠寻找对应相等的边角边相等线段同加同减-对应边2如图2,AE=CF,ADBC∥,AD=CB,求证:⊿ADFCBE≌⊿3、如图,已知AB=AE,AC=AD,BAD=EAC,∠∠证明:∠B=E∠ABCDE证明: ∠BAC=BAD+DAC∠∠∠DAE=EAC+DAC∠∠∠BAD=EAC∠∴∠BAC=DAE∠在△ABC与△ADE中,AB=AE∠BAC=DAE∠AD=AC∴△ABCAEDB=E≌△∴∠∠寻找相等的角相等的两个角同加或同减,得到相等的对应角思考问题.1已知:如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:△ABD≌△ACE.证明: ∠BAC=∠DAE(已知),∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.在△ABD与△ACE中,AB=AC(已知),∠BAD=∠CAE(已证),AD=AE(已知),∴△ABD≌△ACE(SAS).ABDCE求证:1.BD=CE2.∠B=∠C3.∠ADB=∠AEC2.如图,AB平分∠DAC,要用SAS条件确定△ABCADB,≌△还需要有什么条件?ABCDAC=AD寻找相等的对应角角平分线寻找相等的对应边公共边FEDCBA3.如图,已知DC=BF,DE=BA,若使△ABCEDF,≌△还需要补充的条件可以1、边角边公理(SAS)—夹角2、转化思想证线段位置关系(垂直、平行)角平分线求角度数、数量关系角相等证三角形全等SSSSAS线段相等归纳小结:l.利用全等三角形证明线段或角相等,是证明线段或角相等的重要方法之一,其思路如下:⑴观察要证的线段和角分别在哪两个可能全等的三角形之中.⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.⑶设...