12.2.1--全等三角形的判定.2.1-全等三角形的判定--课件--郭丹VIP免费

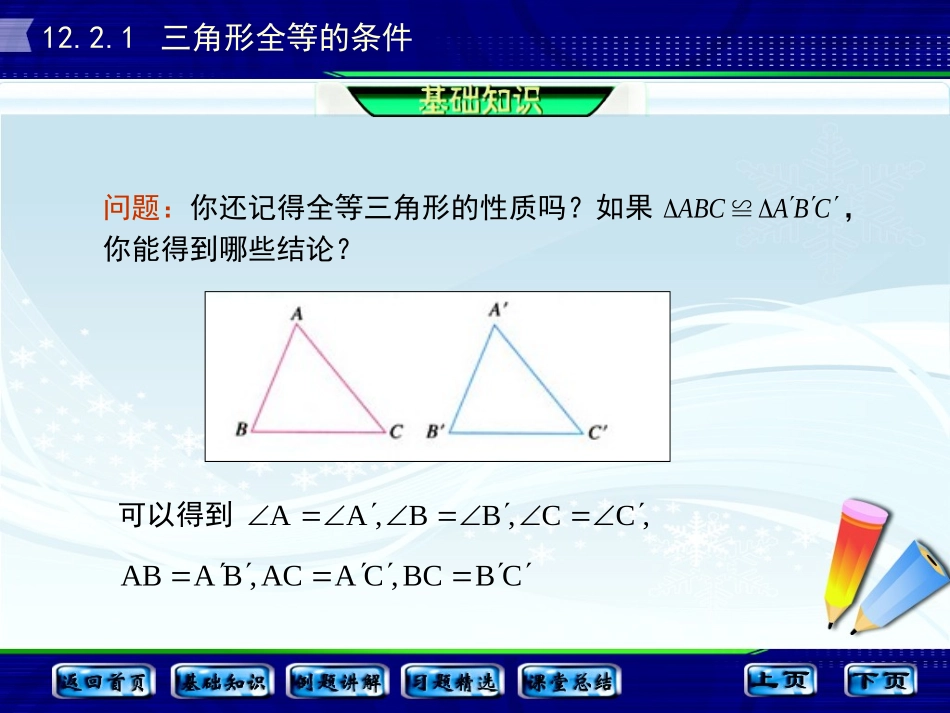
§12.2.1三角形全等的判定12.2.1三角形全等的条件问题：你还记得全等三角形的性质吗？如果，你能得到哪些结论？CBAABC≌可以得到,CC,BB,AACBBC,CAAC,BAAB问题：先任意画出一个，再画一个，使和满足上面六个条件中的一个或两个，与一定全等吗？ABCCBAABCCBAABCCBA问题：和满足上面六个条件中的三个，能保证与一定全等吗？ABCCBACBAABC12.2.1三角形全等的条件(几何画板演示.)情况1先任意画出一个，再画一个，使，它们全等吗？ABCCBABCCBACCAABBA,,画法：（1）画线段；（2）分别以B′,C′为圆心，线段AB,AC为半径画弧，两弧相交于点A′；（3）连接线段得.BCCB,CA,BACBA三角形全等的条件1三边对应相等的两个三角形全等（简写为：“边边边”或“SSS”）.12.2.1三角形全等的条件情况2先任意画出一个，再画一个，使它们全等吗？ABCCBA,,ACCAABBA,AA画法：（1）画∠DA′E=∠A;（2）在射线A′D上截取，在射线A′E上截取；（3）连接B′C′.ABBAACCA两边和它们的夹角对应相等的两个三角形全等（简写为：“边角边”或“SAS”）.12.2.1三角形全等的条件情况3先任意画出一个，再画一个，使，它们全等吗？CBAABC,ABBABBAA,画法：（1）画；（2）在的同旁画，A′D,B′E交于点C′.ABBABABABE,ABAD12.2.1三角形全等的条件三角形全等的条件：两角和它们的夹边对应相等的两个三角形全等.（简写为：“角边角”或“ASA”）两个角和其中一个角的对边对应相等的两个三角形全等.（简写为：“角角边”或“AAS”）情况4先任意画出一个，使∠C=90°,再画一个，使∠C′=90°，，它们全等吗？ABCRtCBARtBCCBABBA,12.2.1三角形全等的条件画法：（1）画；（2）在射线上取；（3）以B′为圆心，AB为半径画弧，交射线C′N于点A′；（4）连接A′B′.90NCMMCBCCB斜边和一条直角边对应相等的两个直角三角形全等（简写为：“斜边、直角边”或“HL”）.12.2.1三角形全等的条件【例1】已知：如图1，AB=AD，BC=CD，求证：△ABC≌△ADC.ABCD图1【答案】证明：在△ABC和△ADC中AB=AD（已知）BC=CD（已知）AC=AC（公共边）∴△ABCADC≌△（SSS）.12.2.1三角形全等的条件【例2】已知：如图2，AB=CB，∠ABD=∠CBD，问AD=CD，BD平分∠ADC吗？AB=BC（已知）∠ABD=∠CBD（已知）BD=BD（公共边）∴△ABC≌△ADC（SAS）∴AD=CD，BD平分∠ADC（全等三角形的对应边相等，对应角相等）.【答案】证明：在△ABD和△CBD中ABCD如图212.2.1三角形全等的条件【例3】已知：如图3，CD⊥AB于点D，BE⊥AC于点E，BE、CD交于点O，且AO平分∠BAC，求证：AD＝AE.【答案】证明：因为CD⊥AB，BE⊥AC，所以∠ADO＝∠AEO＝90°.还因为AO是∠BAC的平分线，所以∠OAD＝∠OAE.在△AOD和△AOE中，ABCDEO图3∠OAD＝∠OAE（已证）AO=AO（公共边）∴△AOE≌△AOD（AAS）.∴AD=AE（全等三角形的对应边相等S）.∠ADO＝∠AEO（已证）12.2.1三角形全等的条件【答案】BD=CD，理由：∵AD⊥BC于点D，∴∠ADB＝∠ADC=90°.在Rt△ABD和Rt△ACD中，AD=AD（公共边）∴Rt△ABD≌Rt△ACD（HL）.∴BD=CD（全等三角形的对应边相等）.AB=AC（已知）【例4】如图4，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上，两个木桩离旗杆底部的距离相等吗？请说明你的理由.BDCA如图412.2.1三角形全等的条件1.如图1所示，已知AC=BD，AD=BC，那么∠C=∠D吗？为什么？图112.2.1三角形全等的条件2.如图2，在四边形ABCD中，AB=CD，∠BAC=90°，∠ACD=90°，求证：AD=BC.ABCD如图212.2.1三角形全等的条件3.已知如图3，点D在AB上，点E在AC上，BE和CD相交于点O，AB=AC，∠B=∠C.求证：△ABE≌△ACD.图3DBEAOC12.2.1三角形全等的条件4.如图4，AC=AD，∠C，∠D为直角，则BC=BD吗？DACB图412.2.1三角形全等的条件用定义来判断三角形全等是非常不方便的，甚至根本无法进行，因此我们研究了怎样用最少的条件，最快捷的方法来证明两个三角形全等.本节课我们从画图、剪纸、验证得到了四种判断三角形全等的方法“SSS”、“SAS”、“ASA”、“HL”，又用“ASA”证明了“AAS”的正确性，从而得到包括直角三角形在内的五种判断方法.12.2.1三角形全等的条件