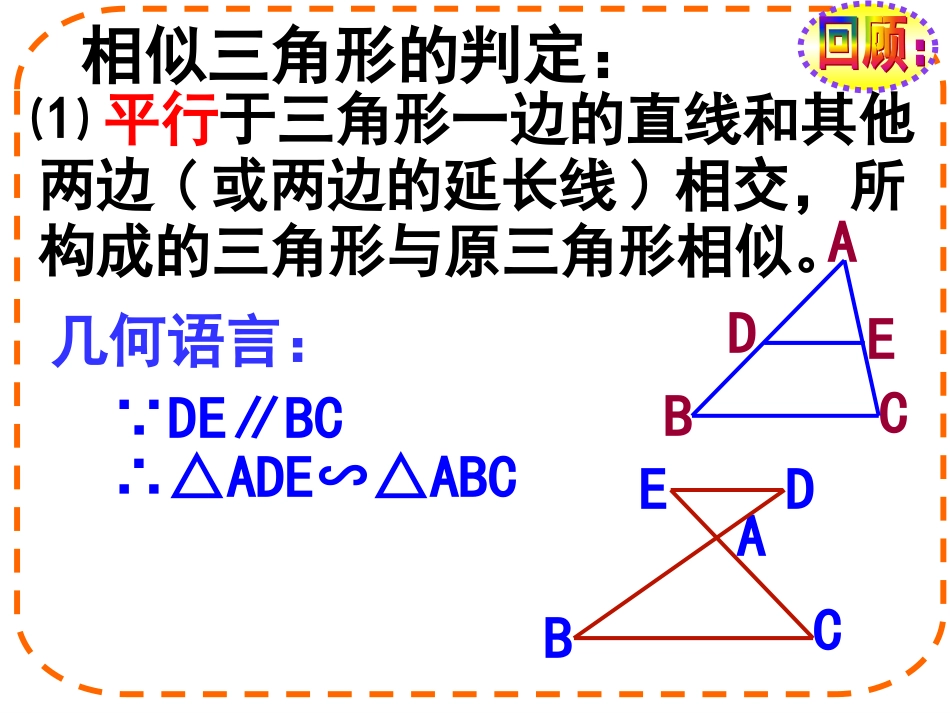
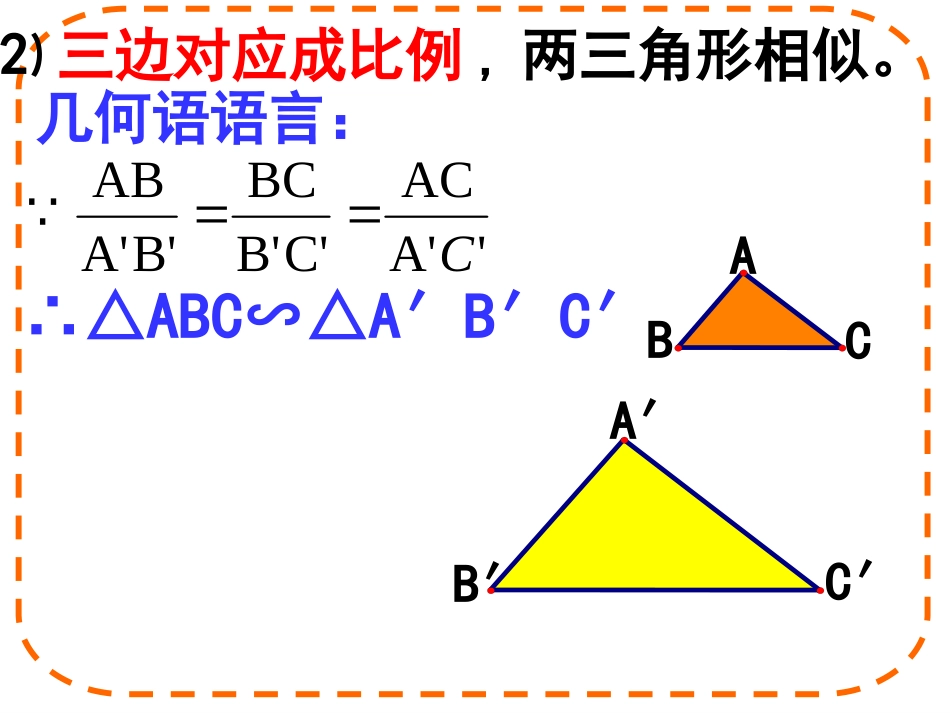
∵DE∥BC∴△ADE∽△ABC⑴平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。EDABCABCDE几何语言:相似三角形的判定:'A'ACC'B'BCB'A'ABC∴△ABC∽△A′B′C′⑵三边对应成比例,两三角形相似。A′B′C′CBA几何语语言:有没有其他办法判断两个三角形相似?注意:①对应角、对应边的书写顺序要与三角形的顺序保持一致。②强调对应顶点要写在对应位置。第二十七章相似27.2.127.2.1相似三角形的判定相似三角形的判定(二)(二)过点D作DE∥B′C′交A′C′于点EA′B′C′证明:在△A′B′C′的边A′B′上截取A′D=AB∴△A′DE∽△A′B′C′∴A′D=AB,A′E=AC∵∠A=∠A′∴△ABC∽△A′B′C′∴△A′DE≌△ABC已知:如图△ABC和△A′B′C′中∠A=∠A′,求证:△ABC∽△A′B′C′。CBAED''''''CAEABADA''''CAACBAAB又''''CAACBAABABMCD结论:两边及其一边所对的角相等,两个三角形不一定相似.ABCABD想一想:如果对应相等的角不是两条对应边的夹角,那么两个三角形是否相似呢?1、已知△ABC和△A′B′C′,根据下列条件判断它们是否相似.(2)∠B=45°,AB=8cm,AC=10cm∠B′=45°,A′B′=16cm,A′C′=20cm.(1)∠A=120°,AB=7cm,AC=14cm,∠A′=120°,A′B′=3cm,A′C′=6cm;∵==1.52、判断图中△AEB和△FEC是否相似?解:∴△AEB∽△FEC∵∠1=∠2==1.5∴=54303645EAFCB12练习:《导学》P152页4、6例2已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=7.5,求AD的长.BCACACAD,25.4解:AB=6,BC=4,AC=5,CD=7.5又∠B=∠ACD,△ABC∽△DCA,AD=应用ACBCCDAB练习:《导学》1、P154页第3题的问改为求证ED垂直AB;2、P155页第6题相似三角形的判定方法有几种?1.定义判定法3.边边边判定法(判定一)4.边角边判定法(判定二)2.平行判定法比较复杂,烦琐只能在特定的图形里面使用小结