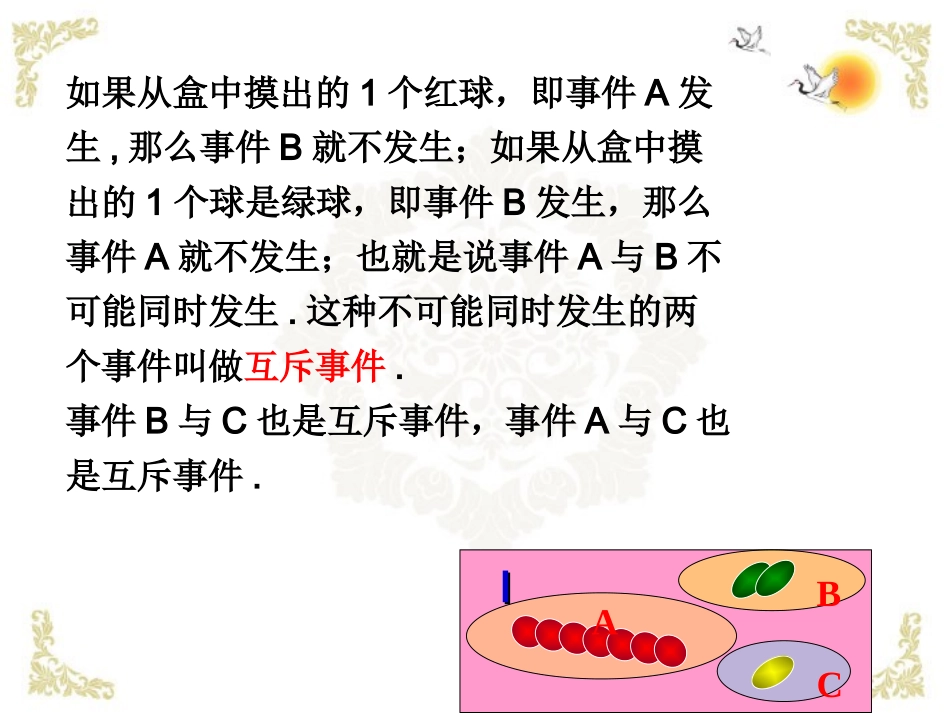
2025年1月21日3.1.4概率的加法公式在一个盒子内放有10个大小相同的小球,其中有7个红球、2个绿球、1个黄球.把“从盒中摸出1个球,得到红球”叫做事件A,“从盒中摸出1个球,得到绿球”叫做事件B,“从盒中摸出1个球,得到黄球”叫做事件C.ABCII如果从盒中摸出的1个红球,即事件A发生,那么事件B就不发生;如果从盒中摸出的1个球是绿球,即事件B发生,那么事件A就不发生;也就是说事件A与B不可能同时发生.这种不可能同时发生的两个事件叫做互斥事件.事件B与C也是互斥事件,事件A与C也是互斥事件.ABCII•对于上面的事件A、B、C,其中任何两个都是互斥事件,这时我们说事件A、B、C彼此互斥.一般地,如果事件A1、A2,…,An中的任何两个都是互斥事件,那么就说事件A1、A2,…,An彼此互斥.•从集合的角度看,几个事件彼此互斥,是指由各个事件所含的结果组成的集合彼此互不相交.ABCII““从盒中摸出1个球,得到的不是红球(即绿球或黄球)”记作事件A从集合的角度看,同事件所含的结果组成的集合,是全集中的事件A所含的结果组成的集合的补集.A由于事件A与不可能同时发生,它们是互斥事件.事件A与必有一个发生.这其中必有一个发生互斥事件叫做对立事件对立事件.事件A的对立事件通常记作.AAAIIAAAABCII•在上面的问题中,“从盒中摸出1个球,得到红球或绿球”是一个事件,当摸出的是红球或绿球时,表示这个事件发生,我们把这个事件记作.现在要问:事件A+B的概率是多少?7272()()()101010PABPAPBABAB()或互斥事件的和事件的概率加法公式由概率的统计定义,可知)()()(BPAPBAP上述结论说明,如果事件A、B互斥,那么事件A∪B发生(即A、B中至少有一个发生)的概率,等于事件A、B分别发生的概率的和。一般地,如果事件A1,A2,…,An彼此互斥,那么事件A1+A2+…+An发生(即A1,A2,…,An中有一个发生)的概率,等于这n个事件分别发生的概率的和,即P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An)•根据对立事件的意义,A+是一个必然事件,它的概率等于1.又由于A与互斥,我们得到P(A)+P()=P(A+)=1即:对立事件的概率的和等于1P()=1-P(A)AAAAA•例1:在数学考试中,小明的成绩在90分以上的概率是0.18,在80—89分的概率是0.51,在70—79分的该律师0.15,在60—69分的概率是0.09,计算小明在数学考试中取得80分以上成绩的概率和小明考试及格的概率?解:(1)分别记小明的考试成绩在90分以上,在80—89分,在70—79分,在60—69分为事件B、C、D、E。(2)因为这四个事件是互斥的,所以可以利用互斥事件的概率加法公式,根据公式得出成绩在80分以上的概率:成绩在60分以上的概率:69.051.018.0)()()(CPBPCBP()()()()()0.180.510.150.090.93PBCDEPBPCPDPE求“小明考试不及格”的概率是多少?•总结一下,本题给我们提出了哪些解题方法与数学思想?•在求较复杂的事件的概率时,通常有两种方法:•一是将所求概率化为一些互斥事件的概率的和来求;•二是若求一个事件的概率,可转化为求其对立事件的概率,体现“正难则反”的数学思想。•归纳出求解方法和步骤,以及应当注意的问题?解题步骤可归纳为4步:(1)引用数学符号表示问题中的有关事件;(2)判断各事件的互斥性;(3)应用概率的加法公式进行计算;(4)写出答案。如果A、B两个事件不互斥,就不能运用互斥事件的概率加法公式。若A、B为互斥事件,才能运用概率的加法公式。•判别下列每对事件是不是互斥事件,如果是,再判别它们是不是对立事件.从一堆产品(其中正品与次品都多于2个)中任取2件,其中:•(1)恰有1件次品和恰有2件次品;•(2)至少有1件次品和全是次品;•(3)至少有1件正品和至少有1件次品;•(4)至少有1件次品和全是正品.巩固练习巩固练习•练习:某人射击一次,命中7~10环的概率如下表所示:•(1)求射击一次,至少命中7环的概率;•(2)求射击一次,命中不足7环的概率;命中环数10环9环8环7环概率0.120.180.280.321.互斥事件定义:不可能同时发生的两个事件。4、概率公式:P(A+B)=P(A)+P(B)如果事件A,B互斥,那么事件A+B发生(即A,B中有...